Introduction
Whenever a material endures variations in contraction or traction longitudinally, Young’s modulus is frequently utilized. It’s a fixed value that aids in defining the elastic characteristics and experiencing real-time contraction or traction. It can measure the compression or tension inside a certain electrical system, making it possible to determine young’s modulus of elasticity of the material of a given wire.
What is Young’s Modulus?
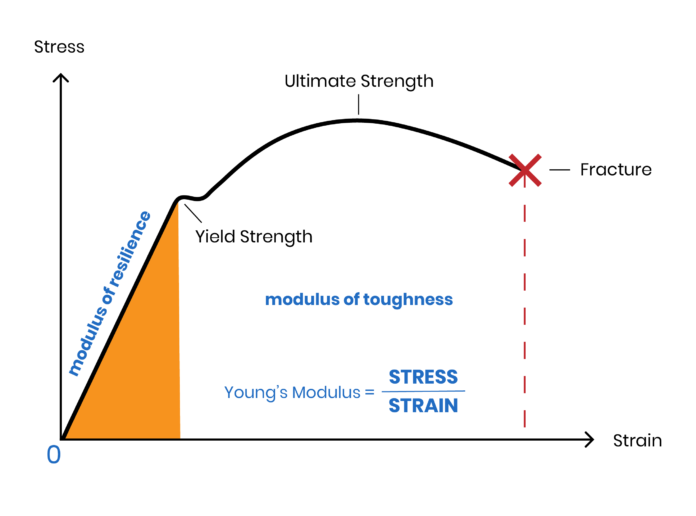
The ratio of tensile stress (σ) to tensile strain (ε) is known as Young’s modulus (E), a feature of the material that indicates how it can easily stretch and flex. Where the stress is the amount of force applied per unit area (σ = F/A) and strain is an extension of per unit length (ε = dl/l).
E = STRESS/STRAIN
E = (F/A)/(dl/l)
Since the force F = mg, we can obtain Young’s modulus of a wire by measuring the change in length (dl) as weights of mass m are applied (assuming g = 9.81 m/s2).
Example – Determine Young’s modulus, when 3 N/m2 stress is applied to produce a strain of 0.15.
Solution – According to the problem, we have
Stress – 3 N/m2
Strain – 0.15
By putting the value in the formula, we find
E=
E = 3/0.15 = 20
Thus, 20 N/m2 is young’s modulus.
Steps of Determination of Young’s Modulus of Elasticity of the Material of a Given Wire
Young’s modulus is a characteristic of a substance that affects the deformation and elasticity of the substance in actual time. It is also described as the proportion of stress to strain, where the stress represents the force applied and gauges the material’s elasticity. Young’s modulus is defined using a curve that takes stress and strain as points of reference, as well as other factors including brittleness, ductility, and plasticity.
Materials required for determining Young’s modulus
The procedure of determining elasticity via Young’s modulus necessitates a number of materials to begin and sustain its integrity. The Instrument of Searle is the most crucial part of this procedure.
It aids in the beginning phases of the decision-making process. Two long steel different wires of similar diameter and length are the next item needed for this technique. This procedure also requires a metre scale and screw gauge for the test’s technical requirements. Following then, a predetermined number of fit weights are used in the calculation procedure. The applied fit weights in this procedure start out at a weight of 0.5 kg. Last but not least, a 1 kg hanger is needed to accurately calculate Young’s modulus in actual time for a specific wire’s elasticity.
Instruments in Searle description
When measuring Young’s modulus in actual time, the instrument of Searle is frequently employed. A small amount of outer force is applied to solid materials when they go through a few elastic deformations. This device seems to be an important component of the building and bridge construction process. The device consists of two wires of equal length coupled to the stiff support.
A spirit level is mounted on the horizontal bar of Searle’s instrument in terms of its physical construction. If the weight on the sides is increased during the identification procedure, the bar that is hung to the control wire extends. Also by slightly turning it inward, the spirit level can be changed. By rotating the screw on a micrometre that is fastened at the place of the test-wire side, one can adjust the tilting within Searle’s instrument.
The process for the identification of elasticity through Young’s modulus
Young’s modulus is used to determine elasticity after a lengthy process that starts with setting up the instrument and ends with recording the findings. Two steel wires must be placed in the proper positions in this method to determine the elasticity. Following that, the hanging and removal processes as well as the wires’ length measuring are commenced. The angle is then established, the screw gauge is maintained, and the wires’ length is measured from middle to end. Then all of the slotted weight needs to be removed, and the spherometer bolt has to be altered. The required processes are then repeated and the observation is noted for further analysis.
Observations
| Sr. no | Linear scale | Circular scale reading | Total reading N+ n×(LC)d (cm) | |
|---|---|---|---|---|
| reading N (cm) | No. of reference line divisions (n) | Value n×(LC) (cm) | N+ n×(LC)d (cm) | |
| 1 | d1 = | |||
| d2 = | ||||
| 2 | d3 = | |||
| d4 = | ||||
| 3 | d5 = | |||
| d6 = | ||||
| 4 | d7 = | |||
| d8 = | ||||
| 5 | d9 = | |||
| d10 = | ||||
FAQs
Q1. What is the SI unit of Young’s Modulus?
Ans. Pascal is the SI unit of Young’s modulus.
Q2. Searle’s apparatus is used for?
Ans. It is used to determine Young’s modulus of elasticity of the material of a given wire.
Q3. What is Young’s modulus?
Ans. It’s a feature of the material that indicates how easily it can stretch and flex.
Q4. What is the crucial element of Young’s modulus approach?
Ans. Searle’s Apparatus is the most critical element of this approach.