Introduction
As a mathematical equation that describes the flow of heat in a given medium, the heat equation has found numerous applications in various fields. From solving problems in engineering to predicting temperature changes in physical systems, the heat equation continues to be a powerful tool in the study of heat transfer. The heat equation is a powerful tool for studying heat transfer in various systems. It has numerous applications in engineering, physics, and biology. However, it has its limitations, which must be taken into account when using it to make predictions. Despite its limitations, the heat equation remains an essential tool for understanding the flow of heat in physical systems.
As per the second law of thermodynamics, heat flows from a body at higher temperature to a body at lower temperature. The rate of heat flow between the bodies depends upon the temperature difference between the bodies and the ability of the material to conduct the heat between them known as thermal conductivity of the material. During the heat transfer between the bodies whether it flows in or out of the body, the heat transfer always occurs in proportion to the amount of heat upon the mass of the material. The proportionality factor in this case is known as the specific heat capacity of the material.
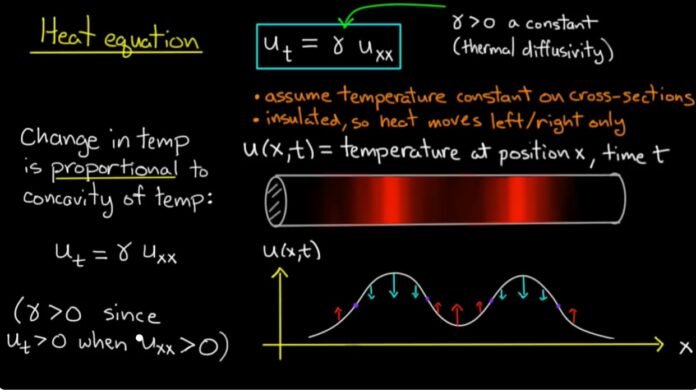
As per the heat equation, the rate of heat transfer in or out of a body is directly related to the temperature of the surrounding material. In other words, the rate of heating or cooling of a body is proportional to how hotter or cooler the surrounding material is. The coefficient of the heat equation alpha takes into consideration all the factors like thermal conductivity, specific heat and the density of the material.
If u is the rate of heat transfer i.e., at what rate a body heats up or cools down, u(x,y,z,t) are specific case of function, then heat equation can be given as:
Where, is called the coefficient of thermal diffusivity of the medium. This equation also explains the flow of heat in an isotropic and homogeneous medium.
The mathematical form of heat equation can also be written as:
This equation represents the parabolic partial differential equation which explains the transfer of heat in a given space over a particular instant of time.
Assumptions in heat equation
1. Specific heat of the body is and it is the quantity of heat required to raise the temperature of a body by degrees, where s is the physical constant determined by the body and m is the mass of the body.
2. The rate of heat transfer is directly proportional to the surface area of the body and the temperature deficit or gradient at the surface of the body. This constant of proportionality is known as thermal conductivity denoted by k.
Derivation of heat equation
The heat equation is a partial differential equation that describes how heat or energy is transferred or distributed over a given space over time. It is also known as the diffusion equation. This equation is used to describe many physical phenomena, ranging from the flow of heat in materials such as metals and liquids to the evolution of species in ecology. The heat equation is expressed mathematically as a partial differential equation, and is defined as the summation of the rate of change of heat with respect to the temperature at each point in the space, multiplied by the thermal diffusivity of the material.
Consider a very small rod with cross-sectional area A and a mass density.
The temperature gradient of the function is given as:
The heat transfer or the rate of heat transferred from the right end of the rod is given as:
Heat transfer from the left end of the rod is given by:
It can be observed that the temperature gradient from both the ends is positive, so the temperature of the body or conductor must increase. S we all know that heat always flows from higher temperature gradient to lower temperature gradient, thus in this case the heat must flow from the right end of the rod to the left side of the rod.
As per the conditions, the equation can be given as:
Where, t is the time period of heat transfer.
The temperature change in the rod can be written as:
We know, the density of the rod is mass upon volume
Now, the heat equation can be written as:
Dividing the both side of the equation by and taking the limits, we get the equation as
The equation can be further represented as :
Where, is called the thermal diffusivity of the rod.
There are so many other ways to derive the heat equation. However, here it is the easiest approach. In detail, we can divide the condition of the constant in three cases, post which we will check the condition in which the temperature decreases, as time increases. It is the phenomena of the heat or any form of energy that they will lose energy while traveling from one medium to the other. Ultimately after the integration, we will get the same equation of the heat in one dimension.
Applications of Heat equation
The heat equation has a wide range of applications in various fields. It is used to analyze heat transfer in materials such as metals and fluids, as well as in ecology to model the evolution of species. It is also used in medical imaging, such as computed tomography, to analyze the distribution of radiation energy in the body.
1.One of the most common applications of the heat equation is in the field of engineering. Engineers use the heat equation to solve problems related to heat transfer in various systems. It helps us in modification of the automobile engines as it helps in determining the specific heat or ability of the engine to absorb or release the heat. It gives us the idea about the rate of heat transfer in an automobile engine. By knowing the ability to absorb heat, we can modify the engines as per the demand and requirement.
2. The transfer of heat from a hot body to a cold body is mostly used in the medical field to relieve the patients from severe pain. It helps in transfer of heat from the hot bottle to the body of the patient which relieves the patient from the pain.
3. The heat equation is used frequently in financial mathematics when modeling options. It can be used to describe a variety of phenomena. The differential equation of the Black-Scholes option pricing model can be converted into the heat equation, allowing for comparatively simple solutions from a well-known body of mathematics. A modeled option price must be obtained by solving many of the extensions to the simple option models numerically because they lack closed form solutions. The heat equation and the equation for pressure diffusion in a porous media share the same basic structure.
4. In physics, the heat equation is used to study the temperature distribution in physical systems. For example, it can be used to determine the temperature distribution in a solid object when it is heated or cooled. It is also used to predict the temperature changes in a fluid when it is heated or cooled. The heat equation is also used in the study of thermodynamics, which is the study of the relationship between heat and other forms of energy.
5. The heat equation is also used in the study of biology. For instance, it can be used to model the temperature distribution in the human body. This is important in medical applications because it can help doctors to determine the temperature changes in different parts of the body. The heat equation is also used in the study of biochemistry, where it is used to model the temperature changes in chemical reactions.
Limitations
While the heat equation is a powerful tool for studying heat transfer, it has its limitations. One of the main limitations is that it assumes that the medium being studied is homogeneous and isotropic. This means that it assumes that the medium has the same properties in all directions. In reality, many materials are not homogeneous or isotropic, which can lead to errors in the predictions made using the heat equation.
Another limitation of the heat equation is that it assumes that the medium being studied is in thermodynamic equilibrium. This means that the temperature is constant throughout the medium. In reality, many systems are not in thermodynamic equilibrium, which can lead to errors in the predictions made using the heat equation.
Recommended Articles:
Derivation of Doppler Effect
Derivation Of Drift Velocity
Derivation of Equation of Motion: Introduction, Methods, And Equations
Derivation of Escape Velocity: Introduction, Formula, And Earth
Hall Effect: Introduction, Theory, Principle, Principle, And Applications
The various modes of heat transfer include Conduction, convection and radiation. A new medium requires a different method to transmit heat from one to the other. When it comes to solids, heat is carried through conduction through the motion of the particles. For liquids and gasses, the mechanism of convection is used to transport heat, which once more involves the transmission of heat from particle to particle. The third one is radiation, with sunlight reaching the earth serving as an example. It is the rate at which the temperature flows through the surface of a material. It measures the transfer of heat from a body at a higher temperature to the body at lower temperature. It is denoted by a symbol and its units are . The value of thermal diffusivity is given by: Where, k is the thermal conductivity, rho is the density of material and s is the specific heat capacity of the material. The movement of molecules in fluids from higher temperature region to lower temperature region is known as convection. Convection can be defined as the process of heat transfer by the bulk movement of molecules within fluids such as gasses and liquids. Initially the transfer of heat takes place through conduction and after the motion of molecules in the fluid increases, the mode of heat transfer shifts towards convection as this transfer of heat takes place due to motion of the fluid. In the derivation of the heat equation, K is denoted for the proportionality constant of the thermal conductivity of the conductor and S is the positive physical constant of heat determined by the conductor given in which the transfer of the heat takes place. We have to take these constants because if we remove the proportionality relation with the direct equation there must be some constant which helps to balance the equation in both the cases. Even during the derivation, there is a constant we have to take so that after putting the values in the given situation there will not be any chance of getting a major difference in the values Heat Equation FAQs
What are the various modes of heat transfer?
Define thermal diffusivity.
What is the movement of molecules in fluids from higher temperature regions to lower temperature regions known as?
What is the use of K and S in the Heat Equation Derivation?