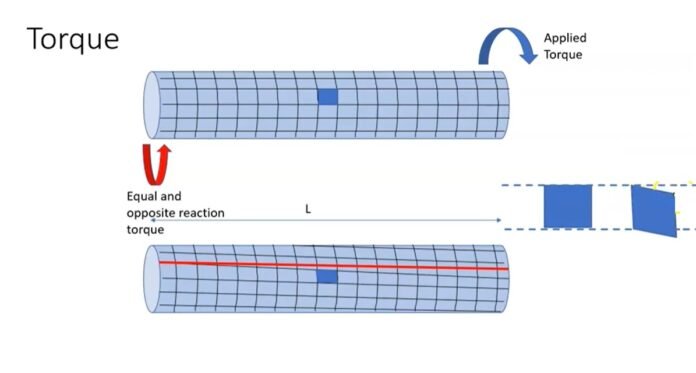
The torsion equation is a fundamental equation in engineering mechanics that describes the deformation of a cylindrical shaft under torsional loading. The equation relates the torque applied to the shaft to the resulting shear stress and angle of twist. The derivation of the torsion equation involves applying the principles of equilibrium and compatibility to a cylindrical element of the shaft.
Torsion Equation
The torsion equation is a fundamental equation in engineering mechanics that describes the deformation of a cylindrical shaft under torsional loading. The derivation of the torsion equation involves applying the principles of equilibrium and compatibility to a cylindrical element of the shaft. The equation relates the torque applied to the shaft to the resulting shear stress and angle of twist. However, the applicability of the torsion equation is limited to situations where the shaft is homogeneous, isotropic, and elastic, and where the assumptions made during the derivation hold true. It is important to keep these limitations in mind when using the torsion equation in real-world applications.
Assumptions
The derivation of the torsion equation is based on several assumptions, which are necessary to simplify the problem and make it solvable. The assumptions include:
- The shaft is made of a homogeneous, isotropic material that behaves elastically.
- The cross-section of the shaft remains flat during deformation.
- The torsional loading is applied gradually, and the shaft is allowed to reach equilibrium at each stage of deformation.
- The shear stress is proportional to the angle of twist, according to Hooke’s law.
Derivation
Consider a cylindrical element of a shaft of radiusand length subjected to torsional loading. Let us assume that the torque applied to the shaft is and the resulting angle of twist is. The shear stress developed in the element due to torsion is
Using the assumptions mentioned above, we can derive the torsion equation by applying the principles of equilibrium and compatibility.
Equilibrium:
The cylindrical element of the shaft is in static equilibrium under the action of the torsional loading. Therefore, the sum of the torques acting on the element must be zero. The torque acting on the element can be expressed as:
Where is the tangential force acting on the element and is the radius of the element. The tangential force can be related to the shear stress by considering a small element of the shaft of length and cross-sectional area The tangential force acting on this element can be expressed as:
Equating the two expressions for, we get:
Where is the shear stress at radius
Compatibility:
The cylindrical element of the shaft undergoes deformation due to the applied torsional loading. The deformation can be expressed in terms of the angle of twist The angle of twist can be related to the shear strain by considering a small element of the shaft of length and cross-sectional area The shear strain in this element can be expressed as:
Using Hooke’s law, we can relate the shear stress to the shear strain as follows:
Where G is the shear modulus of elasticity of the material of the shaft.
Combining the above equations, we get:
Substituting we get:
Integrating both sides, we get:
Where J is the polar moment of inertia of the cross-sectional area of the shaft and is given by:
Limitations:
The torsion equation derived above is valid only under certain conditions.
The assumptions made during the derivation limit its applicability to situations where the shaft is homogeneous, isotropic, and elastic. The equation may not be applicable to situations where the shaft is made of composite materials or undergoes plastic deformation.
Additionally, the torsion equation assumes that the cross-section of the shaft remains flat during deformation, which may not be true for certain types of loading or for non-uniform cross-sections.
Furthermore, the equation assumes that the torsional loading is applied gradually and the shaft is allowed to reach equilibrium at each stage of deformation. This may not be the case in real-world applications, where sudden or dynamic loads may be encountered.
Recommended Articles:
Derivation of Phase rule
Potential Energy: Introduction, Definition, Types, Unit, And Derivation
Derivation Of Prism Formula
Derivation Of Schrodinger Wave Equation
Derivation of the Terminal Velocity
The torsion equation is a fundamental equation in engineering mechanics that describes the deformation of a cylindrical shaft under torsional loading. The assumptions of the torsion equation include: The shaft is made of a homogeneous, isotropic material that behaves elastically. Yes, as it is applicable only if the shaft is homogeneous, isotropic, and elastic. Derivation of Torsion Equation FAQs
What do you understand about the torsion equation?
Write some assumptions of the torsion equation.
The cross-section of the shaft remains flat during deformation.
The torsional loading is applied gradually, and the shaft is allowed to reach equilibrium at each stage of deformation.Are there any limitations in the torsion equation?