In fluid dynamics, the object is moving at terminal velocity if the speed of the object is constant. The reason behind speed being constant is the restraining force that is exerted on an object by the fluid via which that is responsible for its movement. It is possible to change the terminal velocity of an object by the fluid properties, the object’s predicted cross-sectional surface area and the mass of the object.
What is Terminal Velocity
Terminal velocity is defined as the highest velocity attained by a body/object falling through a fluid. It is observed when the sum of buoyancy and drag force equals the downward gravitational force acting on the body/object. The acceleration of the body/object is zero as the net force acting on the body/object is zero.
The formula of Terminal Velocity
Using Mathematical terms, the formula for the derivation of terminal velocity without the buoyancy effects can be described as
Vt =
In the above formula,
Vt= terminal velocity,
g= acceleration of the object because of velocity,
Cd= drag coefficient,
M= mass of a falling object,
P= fluid density via which the object is falling,
A= projected area of the object.
In reality, it is considered that the body/object can attain terminal velocity asymptomatically. The effect of buoyancy is an upward force that is acting on the body/object from the surrounding field. The effect of buoyancy can be considered within the formula using Archimedes’ principle which states that the upward buoyant force that is exerted on a body immersed in a fluid, whether fully or partially, is equal to the weight of the fluid that the body displaces.
Derivation of Terminal Velocity
There is two external forces acting on a body/object which is falling through the fluid. One force is the gravitational force and another one is the drag force.
Gravitational Force: The gravitational force is the force that is exerted as the weight of the body/object. This force is equal to the product of the mass of the falling body/object and the gravitational acceleration.
Weight i.e., W=mg
Here, W is the weight of the body/object,
m is the mass of the body/object and
a is the acceleration.
Drag Force: Drag force which is denoted by D is the force exerted by the fluid stream on the body/object which is falling through it.
D=Cd ρV2A/2
Here, D= drag,
Ρ= density of the fluid,
Cd= drag coefficient,
V= velocity and
A= area projected by the body/object.
The value of drag increases with the square of the velocity of the body/object. For the terminal velocity, the body/object reaches the maximum velocity and the acceleration becomes equal to zero. With zero vertical acceleration, the constant vertical velocity of the body/object is called the terminal velocity.
In this case, the drag becomes equal to weight and there is no external force now acting on the body/object. At terminal velocity, the net force on the body/object becomes equal to zero.
According to the drag equation,
F = bv ²
As b= constant. The value of the constant b is different for different drags.
The freefall of an object is given as,
Σ F = ma
mg -bv ² = m dv/dt
¹/m dr = dv / mg – bv²
Integrating them,
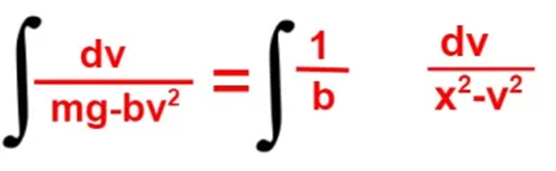
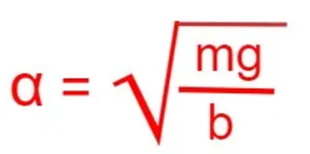
Here,
dv = α sec h² ( Φ ) d Φ
v² = α tan h² (Φ)
After integrating,

v(t) = α tanh ( αb /m × t + arc tanh ( v 0 / α )
by substituting the value of alpha
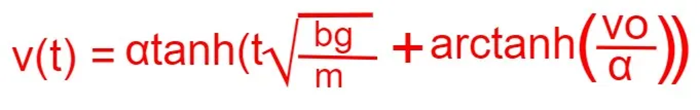
Terminal Velocity in presence of buoyancy
When the effects of buoyancy are considered, then the body/object that is falling through the fluid beneath its own weight can possibly reach the terminal velocity, if the net force that is acting on the specific body/object becomes zero. When this body/object has obtained terminal velocity, the body/object weight gets balanced by the force of upward buoyancy, and the drag force. This is represented as follows:
W = Fb + D
Here,
Fb= buoyancy force,
W= weight,
D = drag force which acts on the body/object.
If the falling body/object has a spherical shape, then expressions for the forces (W, D, Fb) are as follows:
W = (π/6) d3PsG,
D = Cd(½) pV2A
Fb = (π/6) d3PG
The usefulness of Terminal Velocity
When a body/object is dropped from rest, its speed will increase until it reaches at terminal velocity. When a body/object is forced to move faster then its terminal velocity will slow down and upon release, it will reach its constant velocity. Terminal velocity occurs when the speed of a moving object is no longer decreasing or increasing and the object’s acceleration or deceleration is zero.
Recommended Articles:
Derivation Of Orbital Velocity: Introduction, Derivation, Escape, Relation And Factor
Derivation of Phase rule
Potential Energy: Introduction, Definition, Types, Unit, And Derivation
Derivation Of Prism Formula
Derivation Of Schrodinger Wave Equation
Terminal velocity is the maximum velocity attainable by a body/object as it falls through a fluid. The coefficient of drag is the value or quantity of resistance of a body/object falling through a fluid. The factors on which the terminal velocity depends are: Mass of the object Coefficient of drag Density of fluid Acceleration due to gravity, Projected area of the falling object Derivation of the Terminal Velocity FAQs
Define terminal velocity.
Explain the Coefficient of drag.
Enlist the factors on which terminal velocity depends.
