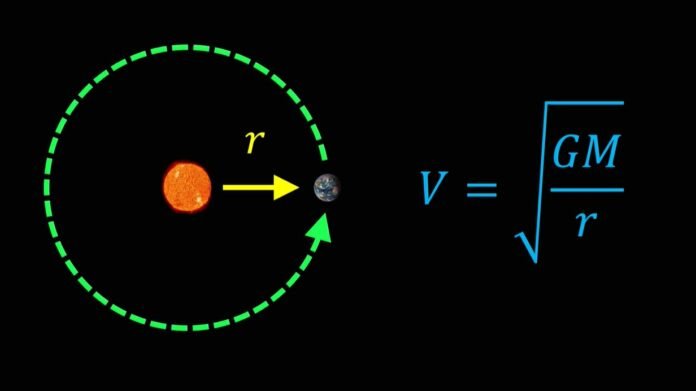
Orbital velocity is the minimum speed required for an object, such as a satellite or spacecraft, to remain in orbit around a celestial body, such as a planet or moon, without being pulled towards it by gravity. It is determined by the gravitational force of the celestial body and the altitude of the object in its orbit. The higher the altitude, the lower the gravitational force, and thus, the lower the orbital velocity required.
Orbital Velocity
Orbital velocity is defined as the velocity by which a body revolves or bend over around the other body. Objects which are travel in the uniform circular motion around the Earth are called it is in the orbit. Orbital velocity depends on the distance between the centre of earth and the object.
Formula for Orbital Velocity is given as-
Vorbital =
Where,
G = gravitational constant.
M = mass of a body.
R = radius of the orbit.
Derivation of Orbital Velocity
For derivation of Orbital Velocity we use
Gravitational Force
Centripetal Force
Gravitational force is the force that allows orbiting to exist. A central body exerts a gravitational force on the orbiting body for keeping it in its orbit. Centripetal force is also important because it is the force responsible for circular motion.
For the derivation
Consider a satellite having mass m which is revolving around the Earth in a circular orbit whose radius r at a height h from the surface of the Earth.
Let M and R are the mass and radius of the Earth respectively,
Then,
r = R + h.
For revolve the satellite centripetal force is given as
mvo2 /r
the gravitational force is given as
G ( Mm/r2)
By comparing both the equations we get
mvo2 /r = G ( Mm/r2)
vo2 = G ( m/r) = GM / R+h
On solving above equation again we get
V0 = ……(equation 1)
But
GM = gR2
g = acceleration due to gravity.
Hence,
V0 =
On solving above equation we get
V0 = R
Let
g’ = acceleration due to gravity.
g’ = GM / (R+h)2
Solving again we get
GM / (R+h) = g’ ( R+h) = g’r ……(equation 2)
From the equation 1 and 2.
V0 = =
Escape Velocity
Escape velocity is the minimum speed an object must have in order to overcome the gravitational pull of a celestial body and escape from its orbit. It is determined by the mass and size of the celestial body, as well as the altitude of the object.
The greater the mass and size of the celestial body, the stronger its gravitational pull and the higher the escape velocity required. The escape velocity for an object on the surface of a celestial body is greater than that for an object at a higher altitude.
Relation Between Orbital Velocity and Escape Velocity
Escape velocity – It is the minimum velocity which is required to overcome the gravitational potential of a body and escape from its orbit.
Orbital velocity – It is the velocity by which an object revolves around a massive body.
The relation between escape velocity and orbital velocity are given as-
V0 = Ve/
Ve = V0
Where,
Ve = Escape velocity.
Vo = Orbital velocity.
We know that-
Escape Velocity = Orbital Velocity
which means, Escape velocity is directly proportional to the Orbital velocity.
Factor affecting Orbital Velocity
Orbital velocity is affected by several factors, including:
Gravitational pull of the celestial body
The greater the mass and size of the celestial body, the stronger its gravitational pull and the higher the orbital velocity required.
Altitude of the object
The altitude of the object in its orbit affects its gravitational force, and thus, its orbital velocity. The higher the altitude, the lower the gravitational force and the lower the orbital velocity required.
Mass of the object
The mass of the object in orbit affects its velocity and stability in orbit. A heavier object will require a higher orbital velocity to counteract its greater gravitational force.
Recommended Articles:
Derivation Of Lens Formula
Derivation Of Lens Maker Formula: Assumptions, Derivation, Applications, And Limitations
Derivation Of Lorentz Transformation: Introduction, Formula, Transformation, And significance
Derivation of Mirror Formula: Terms, Formula, Assumptions, And Derivation
Derivation of the One-Dimensional Wave Equation
Orbital velocity is the minimum speed required for an object, such as a satellite or spacecraft, to remain in orbit around a celestial body, such as a planet or moon, without being pulled towards it by gravity The S.I. unit of orbital velocity is meter per second (m/s) The relation between escape velocity and orbital velocity are given as- V0 = Ve/ Ve = V0 From the equation Escape Velocity = Orbital Velocity Those physical quantity which have magnitude only are scalar quantity while physical quantity which have both magnitude and direction are called vector quantity. Escape velocity is the minimum speed an object must have in order to overcome the gravitational pull of a celestial body and escape from its orbit hence escape velocity is also a scalar quantity. Derivation Of Orbital Velocity FAQs
What is orbital velocity?
What is the SI unit of orbital velocity?
Write the formula which show the relation between orbital velocity and escape velocity?
Does escape velocity belong to a vector or scalar quantity?