Lorentz transformation is a set of equations that describe how measurements of space and time change for an observer in one inertial reference frame when they are compared to measurements made by an observer in a different inertial reference frame that is moving relative to the first.
The Lorentz transformation was first derived by Hendrik Lorentz in 1904, and it forms the basis of Albert Einstein’s theory of special relativity.
The equations describe how space and time intervals between events are altered when viewed by observers in relative motion, and how the fundamental constants of physics, such as the speed of light, are invariant under these transformations.
Lorentz Transformation
The Lorentz Transformation is a set of mathematical equations used in physics to describe how measurements of space and time change for an observer who is moving at a constant velocity relative to another observer.
Lorentz Transformation Formula
The Lorentz transformation formula for transforming the coordinates (x, y, z, t) of an event from one reference frame to another moving at a relative velocity v in the x direction is given as-
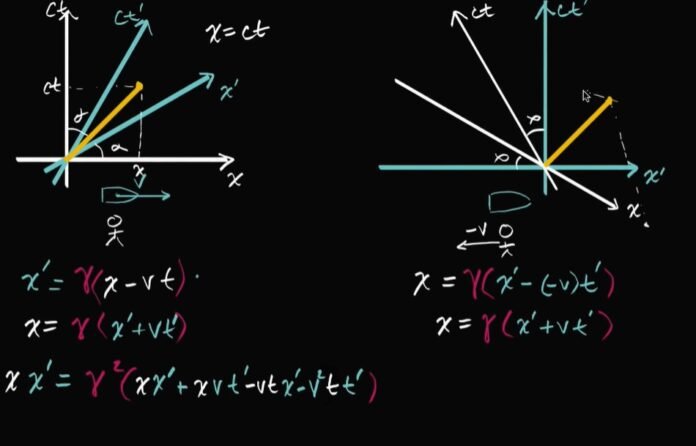
x’ = γ(x – vt)
y’ = y
z’ = z
t’ = γ(t – vx/c2)
where γ is the Lorentz factor:
γ = 1 / (1 – v2/c2)1/2
Here, c is the speed of light in a vacuum and is considered to be a fundamental constant of nature. The Lorentz transformation formula is a fundamental principle of special relativity, which is the theory of physics that describes the behavior of objects moving at speeds close to the speed of light.
Derivation of Lorentz Transformation
x’ = a1x + a2t
y’ = y
z’ = z
t’ = b1x +b2t
The origin of frame x’ = 0, with speed v in frame S. For the beam of light. Let x = vt be the location at time t in frame S.
x’ = 0 = a1x + a2t
x = -(a2/a1)t = vt
Where, a2/a1 = -v
The equation is
x’ = a1x + a2t = a1 (x + (a2/a1)t) = a1(x-vt)
a12 (x-vt2) + y’2 + z’2 – c2(b1x + b2t)2 = x2 + y2 + z2 – c2t2
a1x2 – 2a12xvt + a12v2t2 -c2b12x2 – 2c2b1b2xt – c2b22t2 = x2 – c2t2
(a12 – c2b22)x2 = x2 or a12 – c2b12 = 1
(a12v2 – c2b22)t2 = -c2t2 or c2b22 – a12v2 = c2
(2a12v +2b1b2c2)xt = 0 or b1b2c2 = -a12v
b12c2 = a12 – 1
b22c2 = c2 +a12v2
b12b22c4 = (a12 – 1)(c2 +a12v2) = a14v2
a12c2 – c2 + a4v2 – a12v2 = a14v2
a12c2 – a12v2 = c2
a12(c2-v2) = c2
a12 = c2 / (c2-v2) = 1 / (1- v2/c2)
a2 = -v 1 / (1- v2/c2)½
b12c2 = 1 / (1- v2/c2) – 1
b12c2 = 1- (1 / (1- v2/c2) / (1- v2/c2))
b1 = -v/c2 1 / (1- v2/c2)½
b2 = 1 / (1- v2/c2)½
= 1 / (1- v2/c2)½
We can also write this-
a1 =
a2 = -v
b1 = – (v/c2)
b2 =
The final form of Lorentz transformation
x’ = γ(x – vt)
y’ = y
z’ = z
t’ = γ(t – vx/c2)
Difference Between Galilean and Lorentz transformation
Galilean transformation and Lorentz transformation are two different mathematical frameworks used to describe the behavior of objects in motion, and they are used in different contexts.
Some key differences between the Galilean and Lorentz transformations are –
| Galilean transformation | Lorentz transformation |
|---|---|
| Galilean transformation cannot be used for any casual speed | Lorentz’s transformation is valid for any speed |
| According to Galilean transformation, time is free of the observer and universal. | According to Lorentz transformation time is comparative |
| It assumes that the laws of physics are the same in all inertial frames of reference | Lorentz transformation takes into account the effects of time dilation and length contraction at high speeds. |
| In Galilean transformation, velocities simply add up. | In Lorentz transformation, velocities do not add up in a simple manner due to the effects of time dilation and length contraction. |
Significance of Lorentz transformation
The significance of Lorentz transformation lies in its ability to provide a consistent and universal framework for describing the laws of physics in all inertial reference frames, regardless of their relative motion.
Time dilation: The apparent slowing down of time for moving objects or observers, which is a consequence of the fact that time measurements depend on the relative motion of the observer.
Length contraction: The apparent shortening of objects in the direction of their motion, which is also a consequence of the relativity of motion.
Relativistic mass increase: The increase in the mass of moving objects, which is a consequence of the energy-mass equivalence principle (E=mc2).
Recommended Articles:
Heat Equation: Introduction, Assumptions, Derivation, And Applications
Derivation of Kinetic Energy
Derivation Of Law Of Conservation Of Momentum
Derivation Of Lens Formula
Derivation Of Lens Maker Formula: Assumptions, Derivation, Applications, And Limitations
Lorentz transformation is a mathematical formula that describes how measurements of space and time change from one reference frame to another that is moving relative to the first one at a constant velocity. Lorentz transformation is important because it helps explain the behavior of space and time in special relativity. It shows that measurements of space and time are not absolute but depend on the observer's reference frame. The formula for Lorentz transformation is given by- x' = γ(x - vt) y' = y z' = z t' = γ(t - vx/c2) where γ is the Lorentz factor: γ = 1 / (1 - v2/c2)1/2 Where x and t are the space and time coordinates in one reference frame, x' and t' are the corresponding coordinates in a second reference frame moving at a velocity v relative to the first frame, c is the speed of light. Length contraction is a phenomenon predicted by special relativity, which says that objects appear to be shorter when they are moving relative to an observer. Derivation Of Lorentz Transformation FAQs
What is Lorentz transformation?
Why is Lorentz transformation important?
What is the formula for Lorentz transformation?
What is length contraction in Lorentz transformation?