A famous British scientist Isaac Newton derived three equations of motion that describe the most fundamental concepts of motion of an object and these equations form the backbone of classical mechanics. Classical mechanics is the branch of physics that deals with the motion of bodies under the influence of forces or with the equilibrium of bodies/ objects when all the acting forces are balanced. For all the macroscopic bodies/ objects moving with a speed considerably less than the speed of light, analysis of motion is done using Issac Newton’s Equations of motion.

What are the equations of motion?

Equations of motion are defined as equations that describe the behavior of a system (physical system) in terms of its motion as a function of time. There are three equations of motion in physics used to calculate various parameters such as time, Velocity, acceleration, and Distance. Following are the equations of motion:

First Equation of Motion: v = u + at

Second Equation of Motion: s = ut + ½ at2

Third Equation of Motion: v2 = u2 + 2as

u= initial velocity,

v= final velocity,

t= time,

s= displacement,

a= acceleration

Methods to derive the equation of motion:

Following are the three methods to derive the equations of motion:

Algebraic Method: Derivation using the definition and different formulae of the components of the motion.

Calculus Method: Derivation using the integral method

Graphical Method: Derivation using the graphical representation of the distance, displacement, velocity, and acceleration of an object.

Derivation of the first equation of motion

The first equation relates velocity with the acceleration and time of the body/object. Therefore, this equation is applicable when displacement is not given and this is the reason we call it a velocity-time relation.

The first equation of Motion can be written as:

v_final− u_initial= aΔt

This equation involves the initial and final velocity, time, and constant acceleration. Let a body of mass ‘m’ move with an initial speed i.e., u_initial. The speed of the body changes due to constant acceleration ‘a’ which results in the final speed v_final after a time interval Δt.

Derivation of the first equation of motion by Algebraic Method:

As we know, acceleration of the body/object is defined as the rate of change of velocity.

Mathematically, acceleration is represented as follows:

a

V is final velocity

U is initial Velocity

On rearranging the equation, we can obtain the first equation of Motion, i.e.,

v=u+at

Derivation of First Equation of Motion by Graphical Method:

The first equation of motion can be derived using a velocity-time graph for a moving object with an initial velocity of u, time t, the final velocity of v, and acceleration a.

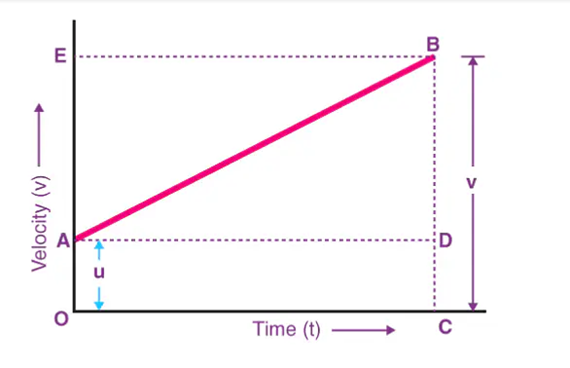
In the graph,

The velocity changes from A to B at a uniform rate in time t.

A perpendicular is drawn from B to OE, A parallel line is drawn from A to D (parallel) and A perpendicular is drawn from B to OC.

OC is t and BC is the v.

The following details are obtained from the graph:

The final velocity of the body i.e., v = BC

The initial velocity of the body i.e., u = OA

From the graph, we can say that

BC = BD + DC

Therefore, v = BD + DC

v = BD + OA since OA = DC

Finally,

v = BD + u (since OA = u)

Let this be equation 1

Now, as we know that the slope of a velocity-time graph is equal to acceleration a.

So,

a = slope of line AB

a = BD/AD

Since AC = AD = t, the equation given above becomes:

BD = at

Let this be equation 2

Now, combining both Equations, the following equation is obtained:

Derivation of the first equation of motion by calculus method:

As we know that acceleration ‘a’ is the rate of change of the velocity, v. Mathematically, we can write

dv/dt=a

dv=adt

adt = ∫vudv

at = v−u

Rearranging it, we get

v= u+at

Derivation of the second law of motion

Second equation: S=uinitial (Δt)+1/2a(Δt)2

It represents the total distances traveled by a body/ object in a time interval of Δt with an initial speed of initial and acceleration ‘a’.

Derivation of Second Equation of Motion by Algebraic Method:

The rate of change of displacement is known as velocity.

Velocity = Displacement/Time

Displacement = Velocity × Time

Use average velocity in place of velocity if the velocity is not constant.:

Displacement=(Initial Velocity + Final Velocity)/2 × Time

s={(u+v)/2} × t

s=[{u+ (u + at)}/2] × t

s=[{2u + at/2}]×t

s=({2u/2} + {at/2})×t

s=(u + ½ at)×t

which can be written as s=ut+½ at2

Derivation of the Second Equation of Motion by the graphical method:

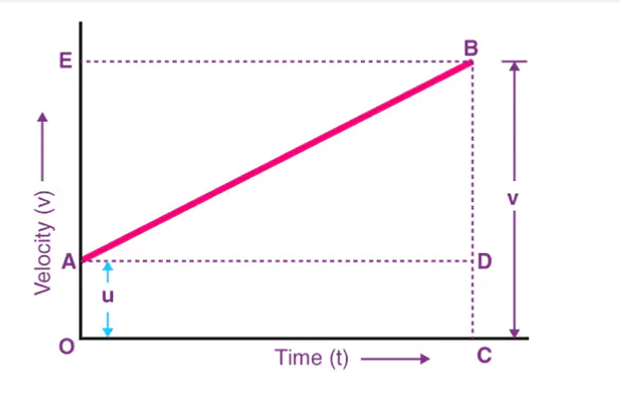
Consider the Figure given above; the total distance traveled by the object in a time interval of Δt is equal to the area of the figure OBCA.

Area of OBCA = Area of rectangle ODCA + Area of triangle ADB

Area of rectangle OEBA = length x breadth

= OA x OB

= Δt×uinitial

Area of triangle CEB = 1/2×base×altitude

1/2×EB×BC

1/2×Δt×(AC−AB)

1/2×Δt×(v_final−uinitial)

1/2×Δt×a(Δt)

1/2×a(Δt)2

Hence, the total distance traveled, ‘s’, is equal to the Area of OECA which is equal to the Area of rectangle OEBA+ Area of triangle CEB and gives the equation

S=uinitial(Δt)+1/2a(Δt)2

Derivation of second equation of motion by calculus method:

Velocity: the rate of change of displacement. Mathematically, this is written as:

ds/dt=v_final

Here ds= the small change in the displacement in a given small interval of time ‘dt’.

v=ds/dt

ds=vdt

ds=(u + at) dt

ds=(u + at) dt = (udt + atdt)

On further simplification, the equation becomes:

∫0sds=∫0tudt+∫0tatdt

s = ut + ½ at2

Derivation of the third equation of motion by the algebraic method:

Let’s assume a body/ OBJECT starts moving with an initial speed of uinitial

and is subject to acceleration ‘a’.

As we know that the second equation of Motion is written as

S=uinitial(Δt)+1/2a(Δt)2

Putting the value of Δt

from the first equation of Motion, which is

Δt=v_final−uinitial/ a

we get the following equation

S=uinitial⟮v_final− uinitial/ a⟯+1/2a⟮v_final−uinitiala⟯2

By solving the above equation, we obtain the third equation of Motion which is

v2final−u2initial=2as

Derivation of the third equation of motion by the graphical method:

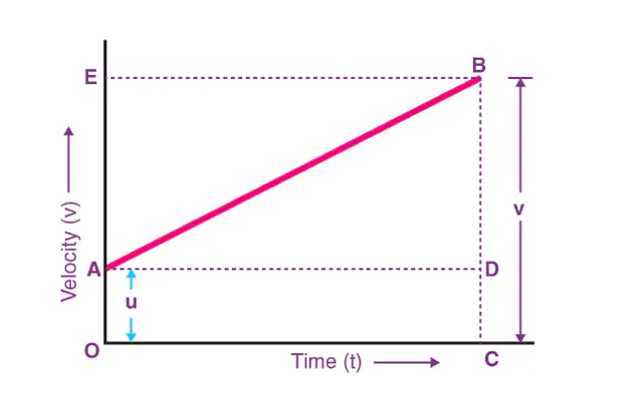
From the above graph, we can say that the total distance travelled, s is given by the Area of trapezium OABC.

Hence,

s = ½ × (Sum of Parallel Sides) × Height

s = 1/2 x (OA + CB) x OC

Since, OA = u, OC = t and CB = v

The above equation becomes

s = 1/2 x (u+v) x t

Now, since t = (v – u)/ a

The above equation can be written as:

s = ½ x ((u+v) × (v-u))/a

Rearranging the equation, we get

s = ½ x (v+u) × (v-u)/a

s = (v2-u2)/2a

The third equation of motion is obtained by solving the above equation:

Recommended Articles:

Centripetal Acceleration: Introduction, Force, Derivation, And Applications
The Compton Effect: Introduction, Experiment, Derivation, Shift, And Confirmation
Derivation Of Continuity Equation: Introduction, Assumption, Applications, And Example
Derivation of Doppler Effect
Derivation Of Drift Velocity