Bending Theory or Timoshenko bending theory suggests that a beam is subject to bending when a force acts upon a point that passes through the longitudinal axis of the beam.

• Therefore, bending theory refers to a study of axial deformation caused due to stresses and is consequently also known as flexure theory.
• The bending equation is a subsection within the purview of bending theory which was given in 1921.

Bending Equation

The bending Equation is given by

σ/y= M/T= E/R

Where,

M is the Bending Moment,

I= Moment of inertia on the axis of bending,

σ is the stress of fibre at distance ‘y’ from the neutral axis in N / mm²,

E is young’s modulus of the material of the beam in N /mm², and

R is the radius of curvature of the bent beam in mm.

In case the distance y is replaced by the element c, then

M/l= σmax/ c

Hence,

σmax = MC/ l= M/ Z

Where,

Z is called the section modulus of the beam and is given by I/ c.

Assumptions of bending equation

The cross-section of the beam is constant and the beam is straight.

The vector sum of all forces acting on the load should be directed in the symmetry planes and this indicates that the forces’ resulting sum should not be in any direction other than the symmetrical planes’ direction.

The cross-section is constant before and after the bending of the beam.

The beam has a symmetrical longitudinal plane and is made of homogenous material.

The elastic limit is the same for tension as well as compression.

Buckling is assumed to be the primary cause of failure.

Derivation of Bending equation

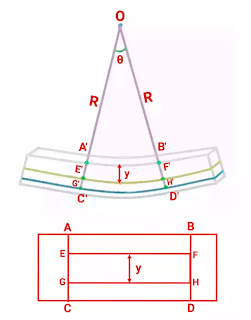
The beam is seen in the second image without any applied pressure and we can see that the beam is not strained. It is also devoid of any flaws. A, B, C, and D, are the four points on the beam where EG= FH is the length. Between the lines EG and FH, the perpendicular distance is y. The beam’s neutral axis is designated as GH and the neutral axis is the point on the beam where there is no tension.

Let us assume that after bending A, B, C, D, E, F, G, and H take positions A’, B’, C’, D’, E’, F’, G’, and H ‘ respectively.

Let,

R = radius of curvature of the neutral,

θ = angle subtended by the beam length at O, and

σ = longitudinal stress

EF = E’F ‘ since, EF is a neutral axis

As we know, Angle = Arc/Radius

So, in ∠OE’F’

θ = E’F ‘/R

E’F ‘ = Rθ

As it is clear in the figure,

EF = GH = E’F’ = Rθ

Again in ∠OG’H’

θ = G’H’/(R+y)

G’H’ = (R+y)θ

Now, Strain in GH

= (Final length – Initial Length)/ Initial Length

= (R+y)θ – Rθ/Rθ

= Rθ + yθ – Rθ/Rθ

= y/R

As we know strain in GH is due to tensile force according to Hooke’s law,

Strain = σ/E

So, Strain in layer GH = σ/E

y/R = σ/E

σ/y = E/R

if E and R Constant

then, σ ∝ y

So, stress is proportional to the distance from the neutral axis.

Now let us consider an elemental area Sa at a distance y from the neutral axis.

So, from the above equation

σ = E/R × y × δa

Now, the force on this element is σ × δa

= E/R × y × δa

The moment of resistance of this elemental force about the neutral axis is given as

(E/R × y × δa) × y

E/R × y ² × δa

The total moment resisted by section M’ is ∫(E/R × y ² × δa)

M’ = E/R ∫( y ² × δa)

Where,

I = ∫( y ² × δa)

The second moment of area of the section or moment of inertia.

So, M’ = (E/R) × I

From equilibrium conditions, we have

M’ = M (applied moment)

So, M = (E/R) × I

M/I = E/R

So, M/I = σ/y = E/R

The above equation is known as the bending equation.

Applications of Bending Stress

• The bending equation is used to find the stress applied to the beam.
• To know the moment carrying capacity of a section.
• For the evaluation of excessive normal stress due to bending.
• For the evaluation of the load-carrying capacity of the beam.

Recommended Articles:

Dc Generator: Introduction, Parts, Work, Equation, Losses, Types, & Applications
Read All About Density of Air
Dependence Of Potential Difference Across A Resistor On Current With Graph
Derivation Of Amplitude Modulation: Introduction, Index, Types, Advantage, And Disadvantage
Derivation of Beer Lambert Law: Statement, Statement, Derivation