In this article, we will discuss the Darcy Weisbach Equation. We will know how the Darcy Weisbach Equation is important in fluid flow. After learning this we will see some real-life examples where Darcy Weisbach Equation plays an important role.

The purpose of this article is to understand the Darcy Weisbach Equation and its derivation. You will also find many other important information that you might need to know. If you do not have time to read all of the information, then I would suggest reading the introduction section first.

Introduction

In fluid dynamics we study the force and acceleration effect on the fluid flow. When fluid flows from a section it contains some resistance to flow due to pipe wall, pressure difference, and its positions. The formula contains Henry Darcy and Julius Weisbach’s names. Darcy Weisbach Equation is used everywhere in fluid dynamics where the friction of fluid particles with the pipe wall is notable.

Head loss in fluid flow

There are following head loss occur in fluid flow:

• Major loss
• Minor loss

Major loss

Pipe friction loss is considered as a major loss in pipe flow. It affects the head loss of the pipe more than the other losses.

Minor loss

Following minor losses are considered in pipe flow.

1. Head loss due to sudden expansion of pipe.
2. Head loss due to sudden contraction of pipe.
3. Head loss at the inlet of pipe
4. Head loss at the outlet of pipe
5. Head loss due to pipe bending.

Assumptions of Darcy Weisbach Equation

Before deriving the formula of Darcy Weisbach Equation we need to take some assumptions. The assumptions we take are the following:

• Fluid flow is continuous and incompressible.
• Fluid flow is steady.
• Dimensions of pipe from which fluid is flow should be uniform and horizontal.

Derivation of Darcy Weisbach Equation

Consider two parts of the pipe, 1 and 2, having the length of L and diameter D. At section 1 fluid velocity is V1 and V2 at section 2. Let pressure at section 1 is greater than section 2 (P1>P2). This will lead to the flow of the fluid from sections 1 to 2.

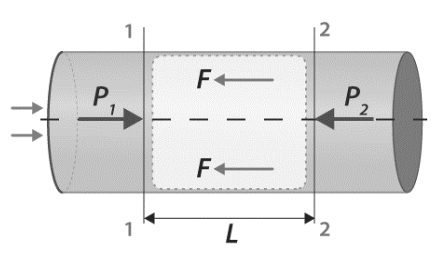
Now, apply Bernoulli’s equation at section 1 and section 2 of the pipe.

Here, P represents the pressure, V represents velocity and Z represent the datum head of the fluid at a specific point. Represent the head loss due to friction of the fluid.

Because the fluid is flowing through the uniform pipe so section 1 and 2 has the same diameter thus from the continuity equation velocity at section 1 is equal to the velocity at section 2.

Now, section 1 and 2 is same height from the datum so

Now Bernoulli equation between the given sections will become

. . . . . . . . . . (1)

Now, the effect of surface roughness and fluid resistance on the velocity of fluid should be considered here. These effects are governed by the Froude’s formula.

Let f’ be the frictional resistance per unit area (wet) per unit velocity.

Frictional resistance F = f’ × wet area × (velocity)²

F = f’ × 2rL × v²

= f’ × . D. L × v²

F = f’ × P’. L × v² . . . . .. . . . (2)

[here, diameter; d= 2r and perimeter; P’=. D]

Force due to friction can be termed as the pressure as following

Now,

From equation (1)

Or,

Now, put

The above equation shows the head loss due to friction in the pipe.

Application of Darcy Weisbach equation

Head loss due to frictional resistance is important to consider as a design parameter of different hydraulic types of machinery such as hydraulic turbine, hydraulic pump, etc. because this is a major head loss so without this the value of net head cannot be calculated.

Recommended Articles:

Curie’s Law: Definition, Formula, Temperature, And Limitations
Current Coil: Introduction, Applications, Specifications, And Difference
Current Density: Introduction, Types, And FAQ
Cyclic Process: Introduction, Types, And FAQ
D’alembert’s Principle: Introduction, Derivation, Examples, And Applications