Curie Weiss Law: Introduction, Limitation, Theory, And FAQ

Introduction

The Curie-Weiss Law, also known as the Curie-Weiss Law of Susceptibility, is a fundamental law in physics that describes the behavior of ferromagnetic materials. It is named after Pierre Curie and his student Pierre-Ernest Weiss, who first proposed the law in the late 19th century.

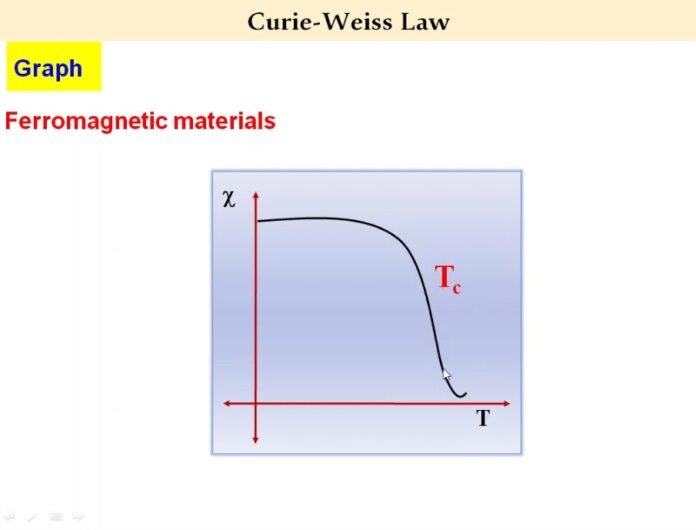
The law states that the magnetic susceptibility of a ferromagnetic material is directly proportional to the inverse of the temperature difference from the Curie temperature (Tc) of the material. The Curie temperature is the temperature at which a ferromagnetic material loses its magnetic properties and becomes paramagnetic.

Mathematically, the Curie-Weiss Law can be expressed as follows:

χ = C/(T – θ)

where χ is the magnetic susceptibility, C is the Curie constant, T is the temperature, and θ is the Curie-Weiss temperature.

The Curie constant C is a material-specific constant that depends on the strength of the magnetic interactions in the material, and the Curie-Weiss temperature θ is a measure of the strength of the exchange interactions between magnetic moments in the material.

The law is based on the assumption that the magnetic moments in a ferromagnetic material are aligned in a parallel manner, and that the magnetic field applied to the material causes a partial alignment of the magnetic moments with the field.

The Curie-Weiss Law is a useful tool in understanding the behavior of ferromagnetic materials, as it allows researchers to predict how a material will behave under certain conditions. For example, the law can be used to predict the magnetic susceptibility of a material at a given temperature, and to estimate the Curie temperature of a new material based on its magnetic properties.

The Curie-Weiss Law has been applied to a wide range of ferromagnetic materials, including metals, alloys, and compounds. It is also used in the development of magnetic storage devices, such as hard drives and magnetic tapes, as well as in the design of magnetic sensors and other devices.

Curie-Weiss Law Limitation

The Curie-Weiss law describes the behavior of a magnetic material in the presence of an external magnetic field. The law states that the susceptibility of the material is directly proportional to the temperature and inversely proportional to the difference between the temperature and the Curie temperature, This is the degree at which the material’s magnetic characteristics change.

However, the Curie-Weiss law has some limitations. One limitation is that it only applies to materials that have a well-defined Curie temperature, which is not true for all magnetic materials. Additionally, the law assumes that the magnetic moments of the atoms in the material are independent of each other, which is not always the case.

Another limitation of the Curie-Weiss law is that it only applies to materials that exhibit paramagnetic behavior, which means that the magnetic moments of the atoms in the material align with an external magnetic field. Materials that exhibit diamagnetic behavior, which means that the magnetic moments of the atoms in the material align in the opposite direction of an external magnetic field, do not follow the Curie-Weiss law.

Moreover, the Curie-Weiss law assumes that the magnetic moments of the atoms in the material are fixed, but this is not true for all materials. In some materials, such as ferromagnets, the magnetic moments of the atoms can interact with each other, leading to complex magnetic behavior that cannot be described by the Curie-Weiss law.

Lastly, the Curie-Weiss law does not take into account the effect of magnetic anisotropy, which is the tendency of a material to have different magnetic properties in different directions. Magnetic anisotropy can be caused by crystal structure, defects, or other factors, and can significantly affect the magnetic behavior of a material. Therefore, the Curie-Weiss law is not applicable to materials that exhibit strong magnetic anisotropy.

While the Curie-Weiss law is a useful tool for describing the magnetic behavior of some materials, it has several limitations and cannot be applied to all materials. Researchers and scientists should be aware of these limitations and use other methods to study the magnetic behavior of materials that do not follow the Curie-Weiss law.

Curie-Weiss Theory

Curie-Weiss theory is a theoretical model in physics that explains the behavior of magnetic materials at high temperatures. It was first proposed by Pierre Curie and then later developed by Peter Weiss.

At high temperatures, the magnetization of a material decreases and eventually disappears. This is due to the random thermal motion of atoms and electrons, which disrupts the alignment of their magnetic moments. Curie-Weiss theory explains this behavior by assuming that the magnetic moments are aligned at low temperatures and that their alignment is disrupted by thermal fluctuations at high temperatures.

The model assumes that the magnetic moments in a material interact with each other through a weak, long-range force known as the magnetic dipole-dipole interaction. The strength of this interaction is characterized by a parameter known as the Curie temperature (Tc). Below Tc, the magnetic moments are aligned in the same direction, resulting in a net magnetization. Above Tc, the thermal fluctuations disrupt this alignment, and the material loses its magnetization.

The Curie-Weiss theory also introduces the Weiss molecular field, which is an average magnetic field that acts on each magnetic moment. This field arises from the interaction between the magnetic moments and their environment, such as the lattice structure of the material. The Weiss molecular field acts to align the magnetic moments, and its strength is related to the Curie temperature.

The theory also predicts the susceptibility of a material, which is a measure of how easily it can be magnetized. The susceptibility is proportional to the inverse of the difference between the temperature and the Curie temperature.

Curie-Weiss theory provides a useful framework for understanding the behavior of magnetic materials at high temperatures. While the model has some limitations, it has been useful for predicting the behavior of many materials and has led to the development of more sophisticated models of magnetism.

What Is Meant By Paramagnetic?

Paramagnetic is a property of certain materials where they exhibit a weak attraction to an external magnetic field. This property arises due to the presence of unpaired electrons in their atomic or molecular orbitals. These unpaired electrons can align their magnetic moment in the direction of an external magnetic field, leading to a net magnetic moment and attraction towards the field.

In paramagnetic materials, the magnetic moments of the unpaired electrons are randomly oriented in the absence of an external magnetic field. However, when an external magnetic field is applied, the electrons align their magnetic moments parallel to the field, leading to a net magnetic moment and attraction towards the field. The strength of the attraction is proportional to the strength of the applied magnetic field.

Some examples of paramagnetic materials include aluminum, platinum, copper, oxygen, and gadolinium. These materials are often used in magnetic applications, such as in magnetic resonance imaging (MRI) machines.

In contrast to paramagnetic materials, diamagnetic materials exhibit a weak repulsion towards an external magnetic field, as all their electrons are paired up and have no net magnetic moment. However, both diamagnetic and paramagnetic materials are generally considered to be non-magnetic, as their magnetic properties are very weak compared to ferromagnetic materials, which exhibit a strong and permanent magnetic moment even in the absence of an external magnetic field.

Recommended Articles:

Coriolis Effect: Introduction, Causes, Demonstration, And Characteristics
Coriolis Effect: Introduction, Effect, Derivation, Characteristics, And Significance
Critical Pressure: Introduction, Point, Substances, And Applications
Critical Velocity: Introduction, Formula,Number, And Calculate
Curie Constant: Introduction, Law, And Constant