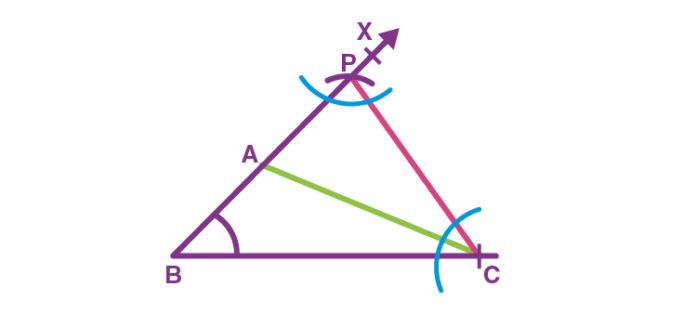
Triangles are one of the most basic shapes in geometry, and their construction is a fundamental skill for any student studying mathematics. Constructing a triangle is not just about drawing three lines, but rather it involves using specific rules and steps to ensure that the triangle is accurately constructed. One such rule is the ASA postulate. In this article, we will explore the ASA postulate and learn how to construct triangles using this method.
ASA Postulate
ASA stands for Angle-Side-Angle, and it is a rule in geometry that states that if two angles and the side between them in one triangle are congruent to two angles and the side between them in another triangle, then the two triangles are congruent.
The ASA postulate can be used to construct triangles in two situations:
- When two angles and the included side are given.
- When two angles and a non-included side are given.
Steps of Construction
Let us now look at the steps involved in constructing a triangle using the ASA postulate:
- Step 1: Draw a line segment AB to represent one of the sides of the triangle.
- Step 2: Using a protractor, construct an angle ∠A, adjacent to side AB.
- Step 3: Measure the length of the other side, AC, using a ruler.
- Step 4: Using a protractor, construct another angle ∠C such that ∠C is congruent to ∠A.
- Step 5: Draw a line segment CD, such that CD is congruent to AC.
- Step 6: Join points B and D to complete the triangle.
Rules to Remember
There are a few rules that you need to keep in mind while constructing triangles using the ASA postulate:
- The two given angles must be adjacent to the side between them.
- The side between the two given angles must be included in the construction.
- The order of the angles is important, i.e., if the given angles are ∠A and ∠C, then they must be used in that order while constructing the triangle.
(Source: GeoGebra)
Examples of Constructing Triangles Using ASA Postulate
Let us now look at a few examples of how to construct triangles using the ASA postulate:
Example 1: Construct a triangle ABC, given that ∠A = 45°, ∠B = 60° and AB = 6 cm.
Solution:
- Step 1: Draw a line segment AB of length 6 cm.
- Step 2: Construct an angle ∠A of 45° adjacent to side AB.
- Step 3: Measure the length of the other side, AC, using a ruler.
- Step 4: Construct another angle ∠C of 75° such that ∠C is congruent to ∠A.
- Step 5: Draw a line segment CD, such that CD is congruent to AC (CD = AB = 6 cm).
- Step 6: Join points B and D to complete the triangle ABC.
Types of Triangles: Based on Sides
Triangles can be classified based on the length of their sides. There are three types of triangles based on sides.
- Equilateral Triangle: An equilateral triangle has three equal sides and three equal angles. The sum of angles in an equilateral triangle is 180 degrees. Each angle in an equilateral triangle is 60 degrees.
- Isosceles Triangle: An isosceles triangle has two equal sides and two equal angles. The third angle is different from the other two angles. The sum of angles in an isosceles triangle is 180 degrees.
- Scalene Triangle: A scalene triangle has no equal sides and no equal angles. The sum of angles in a scalene triangle is 180 degrees.
Types of Triangles: Based on Angles
Triangles can also be classified based on the measure of their angles. There are three types of triangles based on angles.
- Acute Triangle: An acute triangle has three angles that are less than 90 degrees. The sum of angles in an acute triangle is 180 degrees.
- Right Triangle: A right triangle has one angle that is exactly 90 degrees. The other two angles are acute. The sum of angles in a right triangle is 180 degrees.
- Obtuse Triangle: An obtuse triangle has one angle that is greater than 90 degrees. The other two angles are acute. The sum of angles in an obtuse triangle is 180 degrees.
Properties of Triangles
- The sum of angles in a triangle is 180 degrees.
- The exterior angle of a triangle is equal to the sum of the two interior opposite angles.
- In an equilateral triangle, all three angles are equal to 60 degrees.
- In an isosceles triangle, the two equal angles are opposite to the two equal sides.
- The longest side of a triangle is opposite to the largest angle.
- The shortest side of a triangle is opposite to the smallest angle.
Conclusion
The ASA method of constructing triangles is an essential skill that every student must master in geometry. By following the simple steps and rules, students can construct a triangle using two angles and a side. The properties of triangles are crucial in understanding the fundamentals of geometry and its applications in various fields.
Moreover, Physicswallah is an excellent online platform that provides high-quality resources for students who want to learn mathematics and science in an easy and fun way. The platform’s experienced team of educators has a unique teaching style that is tailored to the needs of every student.
Frequently Asked Questions
What is the ASA method for constructing triangles?
The ASA method is a technique used in constructing triangles. It stands for Angle-Side-Angle. This method involves constructing a triangle using two angles and a side between them.
Is the ASA method the only way to construct triangles?
No, there are several methods to construct triangles, including SSS (Side-Side-Side), SAS (Side-Angle-Side), and AAS (Angle-Angle-Side) methods. Each method has its unique steps and rules.
Can a triangle be constructed using any two angles and a side between them?
No, a triangle can only be constructed using two angles and a side between them if the two angles add up to a value less than 180 degrees. If the two angles add up to 180 degrees or more, then no triangle can be constructed.
Are there any properties of triangles that can be applied in constructing them using the ASA method?
Yes, there are several properties of triangles that can be applied in constructing them using the ASA method. The largest angle of a triangle is opposite to the longest side, while the smallest angle is opposite to the shortest side.
Recommended Articles:
CBSE Class 12th Physics Exam Preparation Tips For Students
CBSE Class 11th Physics Exam Preparation Tips For Students
Difference Between Gene and Chromosome, Anatomy, Function, Mechanism
Lymph: What is Lymph? Composition, System, Disorders
Construction of Triangles Using ASA Method, Steps, Rules, Types of Triangles
Construction of Angles: Using Protractor and Compass, Steps of Constructions, Examples
Diffusion Definition, Types, Examples, Factors and Significance