Introduction
We will study structures between points and lines in this section, including how to use a pencil, a ruler, and a set of compasses to create a perpendicular from a point to a line.
How to Construct Perpendicular Lines
Making a line perpendicular to it through a spot
Given: A point P away from the line segment AB.
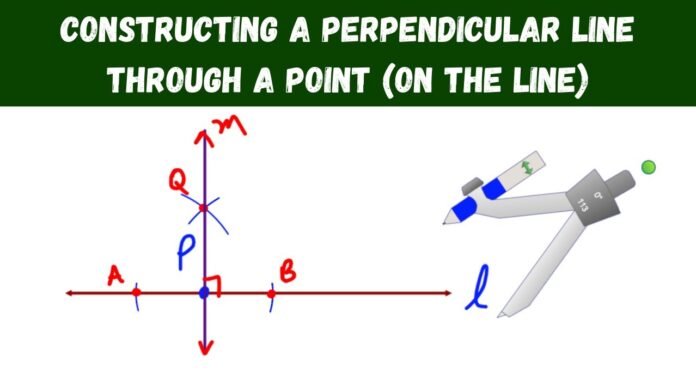
To create a line that is perpendicular to line AB and passes through point P.
Step 1: As indicated in the given picture, draw an arc with P as its centre and any reasonable radius that cuts line segment AB at two different points.
Step 1 in the construction of perpendicular lines
Step 2: Now, draw an arc on either side of the supplied line segment AB using X as the centre and a sufficient radius.Draw an arc on either side of the provided line segment that cuts the arc drawn through point X at P as shown in the above figure, with Y as the centre and the same radius as the previous arc.
Step 2 in the construction of perpendicular lines
Step 3: Connect the points M and P as illustrated, and draw a line segment PQ through point P that is perpendicular to AB if needed.
Step 3 in the construction of parallel lines
Check if the line segment PQ that was created is in fact perpendicular to AB.
As a result, the created line segment PQ is perpendicular to AB. We can easily create two perpendicular lines with a compass and a ruler by utilising the method described above.
How to draw a perpendicular to a line from a given location
Making a perpendicular from a given point to a given line segment entails:
- To cross the line segment, draw two arcs.
- Create two more intersecting arcs.
- Connect the initial point to the intersection of the arcs.
Examples of constructions between lines and points
From a point to a line, for instance
Create a line starting from point P that is perpendicular to the line.
To create the line segment, draw two arcs.
Place the compasses’ point on the initial point P.
Create an arc by crossing the original line twice. They bear the letters A and B.
Create two more intersecting arcs.
Draw another arc by placing the point of the compass on point A, which is where an arc crosses the line. Maintain the same setting for the compasses. Draw another arc to cross the first arc from point B as the centre.
Connect the initial point to the intersection of the arcs.
Connect the intersection point of the arcs with the starting point P using a straightedge (a ruler).
The new line and the original line segment are perpendicular.
AB’s length will likewise have been divided in half by the new line.
Construct Perpendicular Lines FAQs
Q1. How is a 30-degree angle created?
Ans: Construction steps
Create the angle AOD=60 degrees.
Draw the OE of AOD’s bisector.
So, AOE=30.
Q2. In geometry, how is an angle made?
Ans: In Euclidean geometry, an angle is a figure that is created by two rays that share a terminus and are referred to as the angle’s sides and vertices, respectively. Two rays that are in the same plane as each other are used to create angles. Angles can also be created when two planes intersect.
Q3. How are all the angles made?
The compass, ruler, or protractor—which are known as mathematical tools used to construct angles—can be used to create any angle.
Q4. How can I create an angle using a compass?
A compass and a ruler are two geometric instruments that can be used to create an angle. The steps to creating an angle with a compass are as follows:
Draw any part of the line AB.
Draw an arc that intersects the line segment at point S while keeping the compass’ pointed side on A. Any measurement can be used for the compass.
The pointed end is positioned at point S and intersects the first arc at point R while maintaining the same measurement.
Draw a line from point A to point R, linking them using a ruler to create an angle.
The angle can be measured with a protractor.
Q5. How do I use the two-circle method to construct a perpendicular line through a point?
To use the two-circle method, follow these steps:
- Draw a circle with the point as the centre and a radius that is longer than the desired length of the perpendicular line.
- Draw another circle with the same centre point, but with a smaller radius that is equal to the desired length of the perpendicular line.
- The intersection of the two circles will be the endpoints of the perpendicular line. Connect these points with a straight line using the straightedge to complete the construction.
Recommended Articles:
CBSE Class 12th Physics Exam Preparation Tips For Students
CBSE Class 11th Physics Exam Preparation Tips For Students
Difference Between Gene and Chromosome, Anatomy, Function, Mechanism
Lymph: What is Lymph? Composition, System, Disorders
Construction of Triangles Using ASA Method, Steps, Rules, Types of Triangles
Construction of Angles: Using Protractor and Compass, Steps of Constructions, Examples
Diffusion Definition, Types, Examples, Factors and Significance
Construction of Perpendicular Line Through a Point, Steps, How to, Examples