Pendulums have been used for various purposes throughout history, including timekeeping, scientific experimentation, and even art. The accuracy of a pendulum’s period has made it a reliable timekeeping device, with pendulum clocks being used from the 17th century until the 20th century when they were replaced by quartz clocks. Pendulums have also been used in scientific experiments, including the determination of acceleration due to gravity and the study of harmonic motion. A pendulum is a simple device that consists of a weight or mass suspended from a pivot point or fulcrum. It is a classic example of harmonic motion, where the pendulum swings back and forth in a regular and predictable pattern. The time taken for one complete swing of a pendulum is called its period, and this period is dependent on the length of the pendulum.

Introduction:

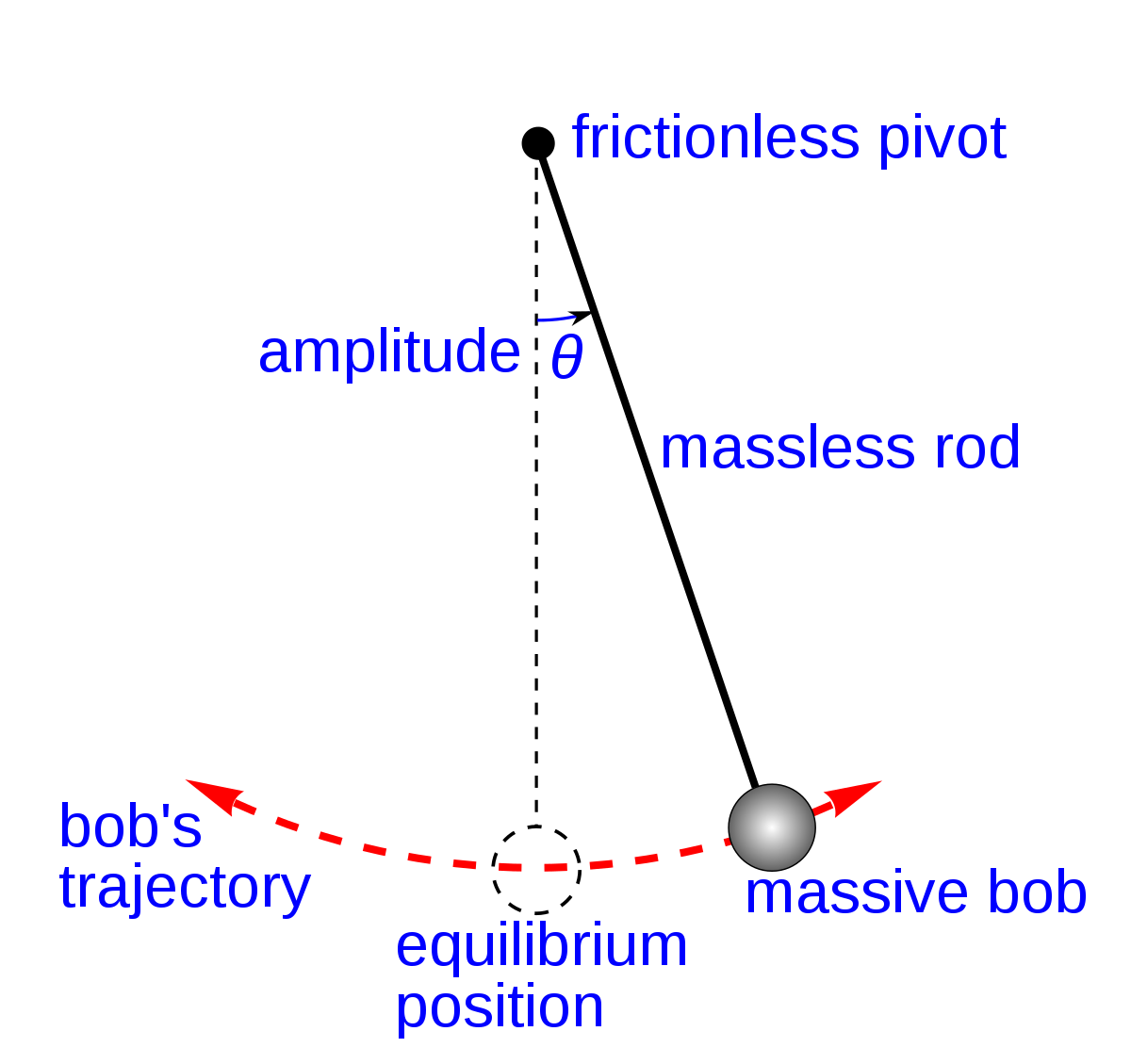
A pendulum is a simple mechanical device that consists of a weight (called a bob) attached to a string or rod, which is suspended from a fixed point. The period of a pendulum is the time it takes for the bob to complete one full swing from one side to the other and back again.

The motion of a pendulum can be explained using the principles of physics. When the pendulum is at rest, the weight is in a state of equilibrium, and there is no net force acting upon it. When the pendulum is released, the weight begins to swing back and forth. The force of gravity acts upon the weight, pulling it downward, while the tension in the string or rod pulls it upward. This creates a restoring force that causes the weight to swing back toward its resting position.

The period of the pendulum:

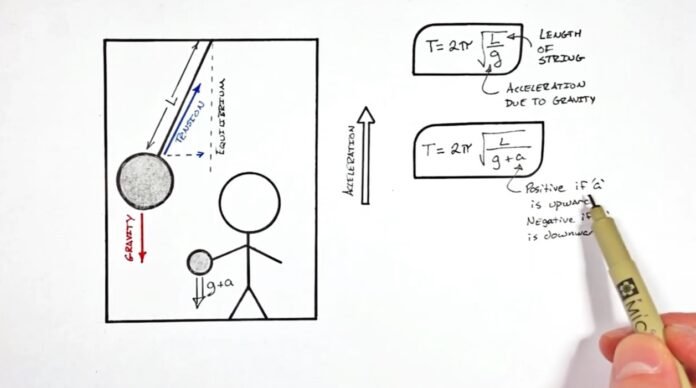
The period of a pendulum depends on several factors, including the length of the pendulum, the mass of the bob, and the acceleration due to gravity. The formula for the period of a pendulum is

T = 2π

where T is the period, l is the length of the pendulum, and g is the acceleration due to gravity.

Derivation of the formula of a period of the pendulum:

To derive this formula, we start by considering the forces acting on the pendulum bob. When the bob is at rest, the force of gravity pulls it downward, and the tension in the string pulls it upward. These two forces are equal in magnitude and opposite in direction, resulting in a net force of zero and a state of equilibrium.

When the bob is displaced from its equilibrium position, the tension in the string changes, creating a restoring force that pulls the bob back toward its equilibrium position. This restoring force is proportional to the displacement of the bob from its equilibrium position, according to Hooke’s Law.

The motion of the pendulum bob can be described by the following differential equation:

+ () sinθ = 0

Where θ is the angular displacement of the pendulum bob from its equilibrium position, t is time, g is the acceleration due to gravity, and l is the length of the pendulum.

This equation can be solved using the small angle approximation, which assumes that the angle θ is small enough that sinθ is approximately equal to θ. With this assumption, the differential equation becomes:

+ ()θ = 0

This is a simple harmonic oscillator equation, which can be solved using the standard solution:

θ = A sin(ωt + φ)

Where A is the amplitude of the oscillation, ω is the angular frequency of the oscillation, and φ is the phase angle.

The angular frequency ω is given by:

ω =

Where T is the period of the pendulum. Substituting this expression for ω into the equation for θ, we get:

θ = A sin(2πt/T + φ)

We can determine the constants A and φ by specifying the initial conditions of the pendulum. For example, if the pendulum is released from a small angle, we can assume that its initial angular displacement is θ = A and its initial angular velocity is dθ/dt = 0. Using these initial conditions, we can solve for A and φ and obtain:

θ = sin(2πt/T)

Now, we can determine the period T by finding the time it takes for the pendulum to complete one full oscillation. This occurs when the angle θ returns to its initial value, so we have:

2π = 2πt/T

Solving for T, we get:

T = 2π

Changing the Period of the Pendulum:

Changing the length of the pendulum is the most common way to change its period. If you increase the length of the pendulum, its period will also increase. Conversely, if you decrease the length of the pendulum, its period will decrease.

This relationship between the length of a pendulum and its period was discovered by Galileo Galilei in the late 16th century. He noticed that the time it took for a pendulum to swing back and forth did not depend on the weight of the bob or the amplitude of the swing, but only on the length of the pendulum.

Changing the mass of the bob will also affect the period of the pendulum. If you increase the mass of the bob, the period will increase. This is because the increased mass will increase the force of gravity on the pendulum, which will slow it down. Conversely, if you decrease the mass of the bob, the period will decrease.

However, changing the mass of the bob is not as common a way of changing the period of a pendulum as changing its length. This is because changing the mass of the bob can also affect the way the pendulum swings, making it more difficult to predict its behavior.

Applications of Pendulum:

While the pendulum may seem like a simple and basic device, it has numerous applications in various fields. Here are some of the most common applications of pendulums:

1. Timekeeping: Pendulum clocks use the back-and-forth motion of a pendulum to keep time. The regular and predictable motion of a pendulum makes it an ideal component for accurate timekeeping.
2. Energy conversion: Pendulums can be used to convert potential energy into kinetic energy and vice versa. For example, a swinging pendulum can be used to power a mechanical clock or generate electricity in a power plant.
3. Scientific experiments: Pendulums are often used in physics experiments to study concepts such as gravity, motion, and harmonic motion. The pendulum’s simple motion and predictable behavior make it an ideal tool for studying these concepts.
4. Motion sensors: Pendulums can also be used as motion sensors in a variety of applications. For example, they can be used to detect earthquakes, measure acceleration, or monitor the vibrations of a machine.
5. Artistic installations: Pendulums can be used as an artistic installation to create interesting and visually appealing displays. They can be used to create mesmerizing patterns, generate sound, or create kinetic sculptures.

Recommended Articles:

Central Force: Definition, Equation, Field, Significance, Properties and Variations
Centripetal Acceleration: Definition, Derivation, Understanding, Applications
Centripetal And Centrifugal Force and Its Component
Change State Solid Liquid Melting Point
Changing States Of Matter And Its Types