Introduction
Acceleration is the rate of change of velocity either in magnitude or direction or in some cases both the magnitude and direction changes. During the circular motion of the body, the direction changes continuously with respect to time, thus acceleration is always associated with a body traversing in a circular path. The external force acting on the body produces acceleration in the body which always points towards the center known as centripetal acceleration. It is always seeking towards the center of the circular path.
Kinematics has taught us that acceleration is a change in velocity, whether it be in speed, direction, or both. Even if the magnitude of the velocity may be constant in uniform circular motion, the direction of the velocity changes continuously, therefore there is always an accompanying acceleration. When you turn a corner in your car, you personally feel this acceleration. (You are in uniform circular motion if you maintain control of the steering wheel during a turn and proceed at a constant speed.) You observe a sideways acceleration as the automobile and you both change lanes. This acceleration will be more obvious the sharper the curve and the faster you are traveling. This section looks at the magnitude and direction of that acceleration.
A shift in velocity can occur in either its magnitude (speed), its direction, or both. Even if the speed may be constant in uniform circular motion, there is always an accompanying acceleration since the direction of the velocity is continually changing. When you turn a corner in your car, you actually experience this acceleration because if you keep the wheel steady and go at a constant speed, you will be moving uniformly in a circle. You observe a sideways acceleration as the automobile and you both change lanes. This acceleration will be more obvious the sharper the curve and the faster you are traveling. We’ll look at the magnitude and direction of the acceleration in this section.
When a body moves in a circular path, the motion associated with it is called the circular motion and the force responsible for a body to move in a circular path is known as centripetal force. During the motion of a body in a circular path, the acceleration vector is always in the direction of center. This property of a body moving in a circular motion which has the acceleration vector always pointed towards the center is called centripetal acceleration. An example of centripetal acceleration is a satellite that orbits around earth in a circular path. The velocity vector in case of centripetal acceleration changes tangentially with respect to time. Thus, we can define centripetal acceleration as the rate of change of velocity tangentially. The net centripetal force acting on a body moving in a circular motion causes centripetal acceleration. The net centripetal force balances the net outward centrifugal force acting on the body, so that the body moves on a circular path and the velocity vector of the motion is always tangential to the motion of the body.
In case of the circular motion of a body, the velocity vector and the force acting towards the center are always perpendicular to each other. If at any instant the velocity of the body moving in circular motion increases or decreases, the net force generated deviates the body from the original path on which it was traversing. If you drive a car around a circle, then your car is undergoing centripetal acceleration and a satellite orbiting the earth also follows a centripetal acceleration. Centripetal means towards the center.
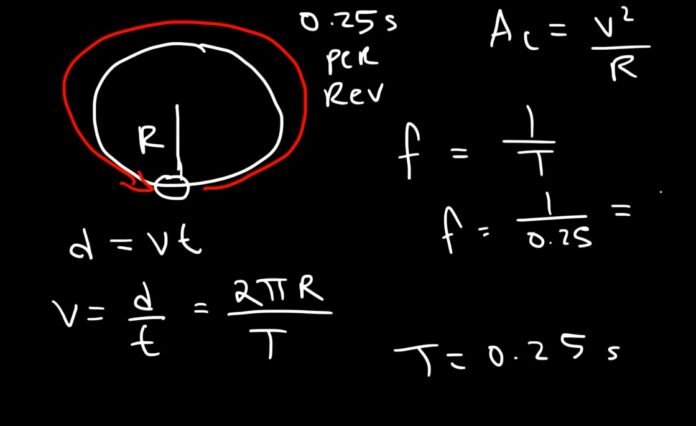
Thus, we can define centripetal acceleration as the magnitude of the ratio of the square of the velocity of the body moving along the circular path to the distance of the body from the center of the circular path on which the body is moving. If a is the centripetal acceleration and v is the velocity of body moving in a circular path and r is the distance of the body from the center of the circle, then centripetal acceleration can be given as :
Where, a is the centripetal acceleration in m/sec2, V is the velocity of the body moving in a circular motion in m/sec and r is the radius of the circle in meters.
Centripetal force
The acceleration that is directed radially towards the center of the circle having a magnitude equal to the square of the speed of the body along the curve is divided by the total distance from the center of the circle to the moving body. The force which causes the acceleration is directed towards the center of the circle and is called a centripetal force.
Centripetal acceleration is a characteristic of an object’s motion along a circular path. Centripetal acceleration applies to any item traveling in a circle with an acceleration vector pointing in the direction of the circle’s center. In your daily existence, you must have encountered numerous instances of centripetal acceleration. A centripetal acceleration occurs when you drive a car in a circle, and a centripetal acceleration also occurs when a satellite orbits the earth. Centripetal refers to being in the middle.
The centripetal force is what causes an object to accelerate in a circular path. It is equal to the mass of the object multiplied by its velocity squared and divided by the radius of the circle. This force is usually provided by an external source, such as a string or a gravitational force.
Centripetal acceleration is caused by the combination of an object’s inertia and gravity. Inertia is the tendency of an object to stay in motion unless acted upon by an outside force. Gravity is the attractive force between two objects with mass. When an object is in circular motion, the inward force of gravity is balanced by the outward force of inertia, resulting in centripetal acceleration.
Derivation of centripetal acceleration
Consider a body of mass m moving in circular motion along the boundary of the circle of radius r and with a velocity v. If a force F is applied on the body, then according to the Newton’s second law of motion:
Where, m is the mass of the body
A is the acceleration produced due to applied force F
As we know, acceleration is the rate of change of velocity with respect to time.
In triangles AOB and PQR, using the properties of similar triangles, we can say that
From the figure, AB=v
We have already known that the rate of change of velocity is the centripetal acceleration.
This is the required equation for calculating the centripetal acceleration of a body moving in a circular motion. The centripetal force keeps a body in a circular motion continuously even if the body is moving with constant velocity. The mathematical derivation of the centripetal acceleration was first presented by Christian Huygens in the year 1659.
The best example of centripetal acceleration is the centrifuge, it is a rotating device that separates the different specimens based on their densities. The high centripetal acceleration provided in the centrifuge decreases the settling time drastically and separates the components in short span of time.Nowadays, the centrifuges are of very much importance as it is very useful in medical researches and various other science projects for making medicines and separation of DNA and proteins.
Centrifuges are often rated in terms of their centripetal acceleration relative to acceleration due to gravity (g); maximum centripetal acceleration of several hundred thousand g is possible in a vacuum. Human centrifuges, extremely large centrifuges, have been used to test the tolerance of astronauts to the effects of accelerations larger than that of Earth’s gravity. A revolving tool called a centrifuge is used to separate specimens of various densities. Little sample separation is made feasible by high centripetal acceleration, which also considerably reduces the time it takes for separation to take place. The separation of macromolecules and single cell suspensions from a liquid medium, including bacteria, viruses, and blood cells, are two common scientific and medical uses for centrifuges.
Applications of Centripetal acceleration
Centripetal acceleration has various applications in everyday life. For example, it is used to explain the motion of a Frisbee as it flies through the air, as well as the motion of a planet around the sun. It is also used to explain why a car turns when driving around a corner. In addition, it can be used to calculate the speed at which an object is moving in a circular path.
Its most common use is in the operation of vehicles, including cars, planes, and boats. When a vehicle is turning, centripetal acceleration allows it to move in a curved path. This same principle is also at work in amusement park rides, which use centrifugal force to create a thrilling experience for riders.
Centripetal acceleration is also used in medical imaging technologies, such as MRI and CT scans. By rotating a patient in a circle, doctors can take detailed images of the internal organs and tissues. This technique has revolutionized the field of medicine, allowing doctors to diagnose and treat conditions with greater accuracy.
Centripetal acceleration is a powerful force that can be harnessed to achieve a variety of goals. Its applications range from entertainment to medical diagnostics, and its implications are far-reaching. Understanding this phenomenon can help us to better appreciate the power of inertia and gravity, and to make use of these forces in our everyday lives.
Recommended Articles:
Dependence Of Potential Difference Across A Resistor On Current With Graph
Derivation Of Amplitude Modulation: Introduction, Index, Types, Advantage, And Disadvantage
Derivation of Beer Lambert Law: Statement, Statement, Derivation
Derivation of Bending Equations: Assumptions, Applications, And Frequently
Derivation Of Biot Savart Law: Application, Importance, FAQ
The dimension formula for centripetal acceleration is the same as that of acceleration. It can be obtained as follows: V=M0L1T-1 R= M0L1T0 The dimensional formula for centripetal acceleration (a)= M0L1T-2 The cause or reason behind the centripetal acceleration is the force that is always pointed towards the center called the centripetal force. It always acts in the direction of the center of the circular path in which the body is moving. Centripetal acceleration is caused by the combination of an object’s inertia and gravity. Inertia is the tendency of an object to stay in motion unless acted upon by an outside force. Gravity is the attractive force between two objects with mass. When an object is in circular motion, the inward force of gravity is balanced by the outward force of inertia, resulting in centripetal acceleration. As we know, in case of the centripetal acceleration the magnitude is constant throughout as the values of both velocity as well as radius is constant. But the velocity is always acting tangentially and changes its direction continuously with respect to time. The direction of the velocity vector is always towards the center. Thus, we can say that the velocity vector changes which in turn changes the centripetal acceleration continuously, which means centripetal acceleration is a variable factor. Centripetal acceleration is a powerful force that can be harnessed to achieve a variety of goals. Its applications range from entertainment to medical diagnostics, and its implications are far-reaching. Understanding this phenomenon can help us to better appreciate the power of inertia and gravity, and to make use of these forces in our everyday lives. Centripetal Acceleration FAQs
What are the dimensions of Centripetal acceleration?
Which force causes centripetal acceleration?
Centripetal acceleration is a constant or a variable vector. Explain?
What are the implications of Centripetal acceleration?