Centripetal Acceleration: Definition, Derivation, Understanding, Applications

Centripetal acceleration is a fundamental concept in physics that describes the acceleration required to keep an object moving in a circular path. It is the acceleration that acts towards the center of a circular path, and it is always perpendicular to the object’s velocity. The term “centripetal” comes from the Latin words “centrum” (center) and “petere” (to seek), meaning “center-seeking.”

Centripetal acceleration is an essential concept in understanding circular motion, which is ubiquitous in everyday life, from the motion of planets and satellites to the motion of vehicles on a curved road. It is also essential in analyzing rotational dynamics and designing systems that involve circular motion and dynamic loads. In this article, we will explore more details about centripetal acceleration and its real-world applications.

Introduction:

Centripetal acceleration is the acceleration experienced by an object moving in a circular path. It is directed toward the center of the circle and is always perpendicular to the velocity of the object. This acceleration is caused by the centripetal force, which is the force that keeps the object moving in a circular path.

To understand centripetal acceleration, we need to first understand the concept of acceleration. Acceleration is the rate at which an object’s velocity changes over time. Velocity is a vector quantity that describes both the object’s speed and direction of motion. Acceleration, therefore, is also a vector quantity and has both magnitude and direction.

Derivation of the formula of Centripetal acceleration:

When an object moves in a circular path, its velocity is constantly changing. This change in velocity causes acceleration, which is directed toward the center of the circle. This acceleration is called centripetal acceleration.

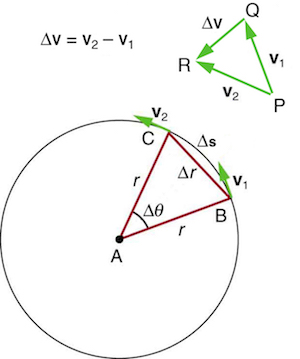
Let us assume an object moving in a circular path with constant velocity. The figure above shows the direction of instantaneous velocity at points B and C. We know that acceleration is the change in velocity. Now, to measure the instantaneous values points B and C must be brought very close to each other making the angle between them infinitely small. In that case, the velocity will point directly toward the center of the circular path.

The magnitude of the centripetal acceleration can be calculated using the formula:

From the figure above it can be observed that the triangles ABC and QPR are isosceles triangles. The two sides of the vector velocity triangles are denoted by v₁ and v₂.

Comparing the two triangles using properties of similar triangles,

——————————–1

Or, ————————-2

We know that acceleration is defined as the rate of change of velocity with respect to time. Dividing both the sides of equation 2 by , we get,

i.e. ———————3

Rearranging the terms of equation 3 we get,

—————————4

Note that Δv/Δt is the ac and Δs/Δt is the tangential speed (v).

Therefore the centripetal acceleration becomes,

Where:

a = centripetal acceleration

v = speed of the object

r = radius of the circular path

The above formula shows that centripetal acceleration is directly proportional to the square of the velocity and inversely proportional to the radius of the circle. This means that as the velocity of the object increases, the centripetal acceleration also increases, and as the radius of the circle increases, the centripetal acceleration decreases.

The SI unit of acceleration is meters per second squared (m/s²). Therefore, the unit of centripetal acceleration is also meters per second squared (m/s²).

The direction of centripetal acceleration is always towards the center of the circle. This is because acceleration is required to keep the object moving in a circular path. If the acceleration did not point toward the center of the circle, the object would move away from the circular path and follow a straight line.

Understanding the Centripetal acceleration:

To understand the concept of centripetal acceleration in more detail, let’s consider a few examples. Suppose you are riding a bicycle around a circular track. As you move around the track, your velocity is constantly changing, even if your speed remains constant. This change in velocity results in acceleration, and this acceleration is centripetal acceleration. The direction of this acceleration is towards the center of the circle, which is why you feel a force pulling you toward the center of the track.

Another example is a satellite orbiting the Earth. The satellite moves in a circular path around the Earth, and its speed and distance from the Earth determine the magnitude of its centripetal acceleration. The direction of the acceleration is towards the center of the Earth, which is what keeps the satellite in its orbit.

Applications of Centripetal acceleration:

Centripetal acceleration has numerous applications in various fields of physics, engineering, and technology. Here are some of the significant applications of centripetal acceleration:

1. Circular Motion: Centripetal acceleration is the force required to keep an object moving in a circular path. It is vital in understanding circular motion, which is ubiquitous in everyday life, from the motion of planets and satellites to the motion of vehicles on curved roads.
2. Vehicle Dynamics: Centripetal acceleration is essential in the design of vehicle dynamics, including cars, trains, and roller coasters. In these systems, the curvature of the track or road provides the necessary centripetal acceleration to keep the vehicle moving in a circular path.
3. Planetary Motion: Centripetal acceleration is crucial in understanding planetary motion, where the gravitational force provides the required centripetal acceleration to keep planets in their respective orbits around the sun.
4. Centrifugal Separation: Centripetal acceleration is used in centrifugal separation techniques, where particles in a liquid or gas are separated based on their mass or density. The centrifugal force generated by the rotation of a centrifuge provides the necessary centripetal acceleration to separate the particles.
5. Particle Accelerators: Centripetal acceleration is used in particle accelerators, such as cyclotrons, synchrotrons, and linear accelerators. In these systems, charged particles are accelerated to high speeds using a magnetic field that provides the necessary centripetal acceleration to keep the particles moving in a circular path.
6. Bridge Design: Centripetal acceleration is also important in the design of bridges and other structures that experience dynamic loads. The design of these structures needs to consider the centripetal force generated by vehicles moving along the curved road to prevent the structure from collapsing.

Recommended Articles:

CBSE Physics Important Questions
Read All About Celestial Bodies
Cell Electromotive Force and Internal Resistance
Celsius And Fahrenheit Difference
Central Force: Definition, Equation, Field, Significance, Properties and Variations