Luna 1, launched in the year 1959, was the first man-made object to attain escape velocity from our planet Earth.
- Escape velocity is the speed that an object requires to escape from the gravitational force of the planet.
- It is the minimum speed with which an object must be launched so that it can overpower the gravitational pull of the planet and hence can escape to space.
- This means the escape velocity should remain constant throughout the way out and must not change while the object is under the influence of the gravitational force of the planet.
What Is Escape Velocity?
The escape velocity or escape speed is the minimum speed needed for a free, non-propelled object to escape from the gravitational influence of a planet, thus reaching an infinite distance from it. It is typically stated as the ideal speed of the object, ignoring atmospheric friction. The escape velocity of an object from the earth is an important factor that is taken into consideration while launching rockets and other space probes, scientists very precisely calibrate the satellites and other space probes to ensure that at no point in time does the velocity of the rocket is higher or lower than the required escape velocity of 11.18 Km/second. Even when the satellites are launched, continuous monitoring is done to ensure the satellites are having the parameters which are necessary for their successful launch.
The formula of the Escape Velocity
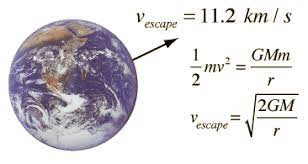
Vescape=√(2GM/R)
Where, G is the gravitational universal constant,
M is the mass of the planet from where the object is thrown, and
R is the radius of the planet
Escape Velocity of Earth
The escape velocity for any planet can be easily calculated if the mass and radius of that planet are known.
For earth, the values of R and g are:
g = 9.8 ms-2 and
R = 63,781,00 m
So, the escape velocity will be:
Vesc= = √2gR= 11.2 km/s
When a spacecraft is launched into outer space, the velocity attained by this should be greater than 11.2km/s so that the rocket does not fall back onto earth.
Derivation of Escape Velocity
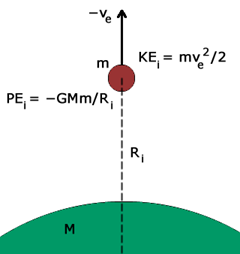
The total energy remains constant for a closed system according to the Law of Conservation of Energy. So, in this scenario, the closed system contains two bodies (the object and the planet) with a gravitational pull between each other. Moreover, no outside force or energy is acting on any of the masses.
Hence,
Total Energy= Total Energy∞
KEi+PEi=0
Kinetic energy= and
Potential energy= GMm/Ri
By substituting the values, we get
( )/2 – GMm/Ri = 0
By adding GMm/Ri on both the sides, we get
( )/2= GMm/Ri
Now foe ve2 we have
ve2 = 2GMm/Ri
By applying square roots on both sides, we get
ve = -√(2GMm/Ri)
as the gravitational convention is away from the other body, so the expression of escape velocity is negative.
Recommended Articles:
The Compton Effect: Introduction, Experiment, Derivation, Shift, And Confirmation
Derivation Of Continuity Equation: Introduction, Assumption, Applications, And Example
Derivation of Doppler Effect
Derivation Of Drift Velocity
Derivation of Equation of Motion: Introduction, Methods, And Equations
The escape velocity which is more accurately referred to as the escape speed is the minimum speed needed for a free, non-propelled object to escape from the gravitational influence of a planet, thus reaching an infinite distance. It is typically stated as the ideal speed of the object, ignoring atmospheric friction. The term escape velocity is a misnomer and it is more accurately referred to as escape speed since the necessary speed is a scalar quantity which is independent of direction. The sum of kinetic energy and potential energy is negative and due to this the velocity is less than the escape velocity the satellite is bound due to the gravitational field of the earth. Hence the total energy is negative. Vescape=√(2GM/R) Where, G is the gravitational universal constant, M is the mass of the planet from where the object is thrown, and R is the radius of the planet The escape velocity for any planet can be easily calculated if the mass and radius of that planet are known. For earth, the values of R and g are: g = 9.8 ms-2 and R = 63,781,00 m So, the escape velocity will be: Vesc= = √2gR= 11.2 km/s When a missile is launched into outer space, the velocity attained by this should be greater than 11.2km/s so that the rocket does not fall back onto earth. Derivation of Escape Velocity: Introduction, Formula, And Earth FAQs
Define escape velocity
When a spacecraft is launched into outer space, the velocity attained by this should be greater than 11.2km/s so that the rocket does not fall back onto earth.Is Escape velocity a scalar quantity?
What is the sum of its kinetic and potential energy when a satellite is launched with a velocity less than the escape velocity?
What is the formula for Escape Velocity?
What is the escape velocity of Earth?