Introduction
A vector is a quantity that has both magnitude and direction. The addition of vectors is the process of combining two or more vectors to produce a single vector. This process is essential in solving many problems in physics. In this article, we will discuss the concept of vector addition, the different methods of vector addition, and some real-world examples of vector addition.
Vector
Vectors are a fundamental concept in physics and play a critical role in understanding and analysing various physical phenomena. A vector is a quantity that has both magnitude and direction. Examples of vectors include force, velocity, and acceleration. Vectors are represented graphically using arrows, where the length of the arrow represents the magnitude of the vector and the direction of the arrow represents the direction of the vector.
Concept of Vector Addition
Vector addition involves adding the magnitudes of two or more vectors to obtain the resultant vector, which represents the net effect of the combined vectors. The direction of the resultant vector is determined by the direction of the individual vectors.
In two-dimensional vector addition, individual vectors are added using the head-to-tail method. To do this, the tail of the second vector is placed at the head of the first vector, and the tail of the third vector is placed at the head of the second vector, and so on. The resultant vector is then drawn from the first vector’s tail to the last vector’s head.
In three-dimensional vector addition, individual vectors are added using the parallelogram method. To do this, the vectors are represented graphically as arrows in a three-dimensional space, and a parallelogram is drawn using the vectors as adjacent sides. The diagonal of the parallelogram represents the resultant vector.
Methods of Vector Addition
There are several methods of vector addition, including graphical, algebraic, and trigonometric methods.
Graphical Method
The graphical method involves representing the vectors graphically using arrows and adding them head-to-tail. The resultant vector is then drawn from the first vector’s tail to the last vector’s head. This method is useful for visualising the vectors and understanding the direction and magnitude of the resultant vector.
Algebraic Method
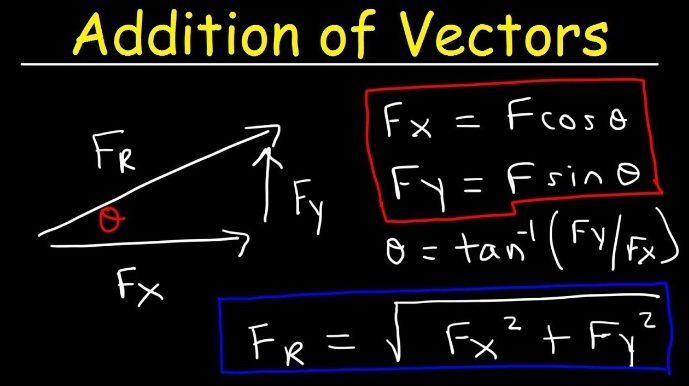
The algebraic method involves representing the vectors using their components along the x, y, and z axes. The x, y, and z components of each vector are added separately to obtain the x, y, and z components of the resultant vector. The magnitude and direction of the resultant vector can then be determined using the Pythagorean theorem and trigonometric functions.
Trigonometric Method
The trigonometric method involves representing the vectors using their magnitudes and angles with respect to a reference axis. The magnitudes and angles are then used to calculate the x, y, and z components of the vectors. The x, y, and z components of the vectors are then added separately to obtain the x, y, and z components of the resultant vector. The magnitude and direction of the resultant vector can then be determined using the Pythagorean theorem and trigonometric functions.
Real-World Examples of Vector Addition
Vector addition is used in many real-world applications, including navigation, engineering, and physics.
Navigation
Navigation is an example of vector addition used in real-world applications. When a plane or ship travels through the air or water, it must take into account the velocity and direction of the wind or current. The speed and direction of the wind or current are vectors that must be added to the rate and direction of the plane or ship to determine the resultant velocity and direction. This is essential for calculating the time and distance of the journey.
Engineering
Engineering is another example of vector addition used in real-world applications. When building a structure, engineers must consider the forces acting on the structure. The forces acting on the structure are vectors that must be added to determine the resultant force acting on the structure. This is essential for ensuring that the structure is stable and can withstand the forces acting on it.
Physics
Physics is a field where vector addition is used extensively. For example, when an object is subjected to multiple forces, the individual forces can be represented as vectors, and the resultant force can be calculated by adding the individual vectors. This is essential for understanding the motion of the object and predicting its future position and velocity.
Another example where vector addition is used in physics is in calculating electric fields. Electric fields are vectors that describe the direction and magnitude of the force experienced by a charged particle in the presence of other charged particles. The electric field at a point in space is the vector sum of the electric fields produced by all the charged particles in the vicinity of that point.
Recommended Articles:
Actions of Transistor Based on Construction
Acoustics | Properties, Propagation, & Scale
Principle & Working Of Accelerometer
Accuracy and precision measurement
Accuracy Precision Error Measurement
A vector is a mathematical representation of a physical quantity that has both magnitude (size) and direction. Examples of vectors include force, velocity, and displacement. To add vectors, their magnitudes, and directions must be determined and the appropriate method of vector addition must be used. This can be done using graphical methods, algebraic methods, or trigonometric methods. Vector addition is important in physics because it enables the calculation of the net effect of multiple vectors acting on a system. This is essential for understanding and predicting the behaviour of physical systems and is used extensively in fields such as engineering and navigation. Scalar quantities have only magnitude (size), while vector quantities have both magnitude and direction. Examples of scalar quantities include mass, temperature, and time, while examples of vector quantities include force, velocity, and acceleration. To improve one's understanding of vector addition in physics, one can practice solving problems involving vectors and use visualisation tools such as vector diagrams to help one understand the concepts better. Seeking help from a physics tutor or teacher can also be beneficial if they are struggling to grasp the concepts. Addition of Vectors FAQs
What is a vector?
How are vectors added?
Why is vector addition important in physics?
What is the difference between scalar and vector quantities?
How can one improve their understanding of vector addition in physics?